【题目】某公司为获得较好的收益,每年要投入一定资金用于广告促销,经调查,每年投入广告费![]() (百万元),可增加销售额约为
(百万元),可增加销售额约为![]() (百万元)(
(百万元)(![]() )
)
(1)若该公司当年的广告费控制在4百万元之内,则应该设入多少广告费,才能使该公司获得的收益最大?
(2)现该公司准备共投入6百万元,分别用于广告促销售和技术改造,经预测,每设入技术改造费![]() (百万元),可增加销售额约为
(百万元),可增加销售额约为![]() (百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益
(百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益![]() 销售额
销售额![]() 成本)
成本)
参考答案:
【答案】(1) 该公司应该投入3百万元用于广告宣传,所获得的收益最大;(2) 该公司投资3百万元用于广告促销,3百万元用于技术改造,可以获得最大有益.
【解析】试题分析:(1)设投入t(t百万元)的广告费后增加的收益为f(t)根据收益为销售额与投放的差可建立收益模型为:f(t)=![]() ,再由二次函数法求得最大值.
,再由二次函数法求得最大值.
(2)根据题意,若用技术改造的资金为x(百万元),则用于广告促销的资金为![]() (百万元),则收益模型为:
(百万元),则收益模型为: ![]() ,因为是高次函数,所以用导数法研究其单调性和极值,最终求得最大值.
,因为是高次函数,所以用导数法研究其单调性和极值,最终求得最大值.
(Ⅰ)广告费![]() ,由此产生的收益
,由此产生的收益![]()
当![]() 时,
时, ![]() 最大,也即该公司应该投入3百万元用于广告宣传,所获得的收益最大.
最大,也即该公司应该投入3百万元用于广告宣传,所获得的收益最大.
(Ⅱ)设6百万元投资中有![]() 百万用于技术改造,
百万用于技术改造, ![]() 百万用于广告宣传,则公司由此产生的收益为
百万用于广告宣传,则公司由此产生的收益为![]()
![]() ,
,
对![]() 求导数,
求导数, ![]() ,当
,当![]() 时,
时, ![]() 最大,
最大,
所以该公司投资3百万元用于广告促销,3百万元用于技术改造,可以获得最大有益.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)是R上的偶函数,且当x≤0时,f(x)=log
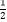 (1﹣x)+x.
(1﹣x)+x.
(1)求f(1)的值;
(2)求函数y=f(x)的表达式,并直接写出其单调区间(不需要证明);
(3)若f(lga)+2<0,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,P,Q分别是BC和CD的中点.
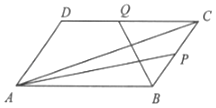
(1)若AB=2,AD=1,∠BAD=60°,求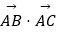 及cos∠BAC的余弦值;
及cos∠BAC的余弦值;
(2)若 =λ
=λ  +
+  ,求λ+μ的值.
,求λ+μ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)是二次函数,方程f(x)=0有两相等实根,且f′(x)=2x+2
(1)求f(x)的解析式.
(2)求函数y=f(x)与y=﹣x2﹣4x+1所围成的图形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
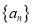 各项均为正数,其前
各项均为正数,其前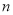 项和为
项和为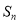 ,且
,且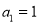 ,
, 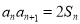 .
.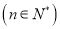
(Ⅰ)求数列
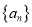 的通项公式;
的通项公式;(Ⅱ)求数列
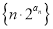 的前
的前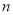 项和
项和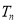 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}满足:a1=
 ,前n项和Sn=
,前n项和Sn=  an ,
an ,
(1)写出a2 , a3 , a4;
(2)猜出an的表达式,并用数学归纳法证明.
相关试题

