【题目】在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
参考答案:
【答案】解:设箱底边长为xcm,则箱高 ![]() cm,得箱子容积
cm,得箱子容积 ![]() (0<x<60).
(0<x<60). ![]() (0<x<60)
(0<x<60)
令 ![]() =0,
=0,
解得 x=0(舍去),x=40,
并求得V(40)=16 000
由题意可知,当x过小(接近0)或过大(接近60)时,箱子容积很小,因此,16 000是最大值
答:当x=40cm时,箱子容积最大,最大容积是16 000cm3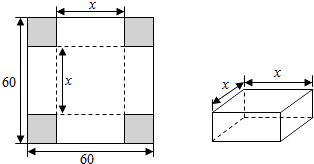
【解析】先设箱底边长为xcm,则箱高 ![]() cm,得箱子容积,再利用导数的方法解决,应注意函数的定义域.
cm,得箱子容积,再利用导数的方法解决,应注意函数的定义域.
【考点精析】解答此题的关键在于理解基本不等式在最值问题中的应用的相关知识,掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)是二次函数,方程f(x)=0有两相等实根,且f′(x)=2x+2
(1)求f(x)的解析式.
(2)求函数y=f(x)与y=﹣x2﹣4x+1所围成的图形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为获得较好的收益,每年要投入一定资金用于广告促销,经调查,每年投入广告费
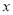 (百万元),可增加销售额约为
(百万元),可增加销售额约为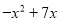 (百万元)(
(百万元)(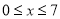 )
)(1)若该公司当年的广告费控制在4百万元之内,则应该设入多少广告费,才能使该公司获得的收益最大?
(2)现该公司准备共投入6百万元,分别用于广告促销售和技术改造,经预测,每设入技术改造费
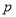 (百万元),可增加销售额约为
(百万元),可增加销售额约为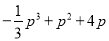 (百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益
(百万元),请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益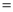 销售额
销售额 成本)
成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
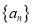 各项均为正数,其前
各项均为正数,其前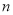 项和为
项和为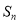 ,且
,且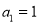 ,
, 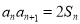 .
.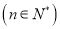
(Ⅰ)求数列
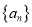 的通项公式;
的通项公式;(Ⅱ)求数列
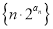 的前
的前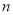 项和
项和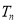 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}满足:a1=
 ,前n项和Sn=
,前n项和Sn=  an ,
an ,
(1)写出a2 , a3 , a4;
(2)猜出an的表达式,并用数学归纳法证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax﹣1(a>0,且a≠1),当x∈(0,+∞)时,f(x)>0,且函数g(x)=f(x+1)﹣4的图象不过第二象限,则a的取值范围是( )
A.(1,+∞)
B.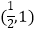
C.(1,3]
D.(1,5] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
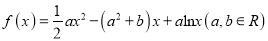
(Ⅰ)当
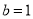 时,求函数
时,求函数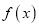 的单调区间;
的单调区间; (Ⅱ)当
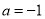 ,
,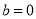 时,证明:
时,证明: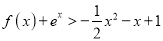 (其中
(其中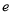 为自然对数的底数).
为自然对数的底数).
相关试题

