【题目】在四棱锥P﹣ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,AD=6,PA⊥底面ABCD,E是PD上的动点.若CE∥平面PAB,则三棱锥C﹣ABE的体积为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解:以A为原点,AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系, A(0,0,0),B(0,2,0),C(2,2,0),D(6,0,0),P(0,0,3),
设E(a,0,c), ![]() ,则(a,0,c﹣3)=(6λ,0,﹣3λ),
,则(a,0,c﹣3)=(6λ,0,﹣3λ),
解得a=6λ,c=3﹣3λ,∴E(6λ,0,3﹣3λ),![]() =(6λ﹣2,﹣2,3﹣3λ),
=(6λ﹣2,﹣2,3﹣3λ),
平面ABP的法向量 ![]() =(1,0,0),
=(1,0,0),
∵CE∥平面PAB,∴ ![]() =6λ﹣2=0,
=6λ﹣2=0,
解得 ![]() ,∴E(2,0,2),
,∴E(2,0,2),
∴E到平面ABC的距离d=2,
∴三棱锥C﹣ABE的体积:
VC﹣ABE=VE﹣ABC= ![]() =
= ![]() =
= ![]() .
.
故选:D.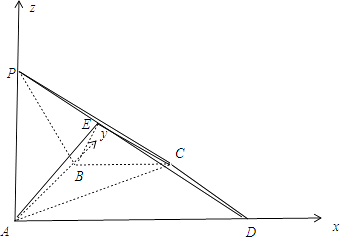
以A为原点,AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出三棱锥C﹣ABE的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}满足:a1=
 ,前n项和Sn=
,前n项和Sn=  an ,
an ,
(1)写出a2 , a3 , a4;
(2)猜出an的表达式,并用数学归纳法证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax﹣1(a>0,且a≠1),当x∈(0,+∞)时,f(x)>0,且函数g(x)=f(x+1)﹣4的图象不过第二象限,则a的取值范围是( )
A.(1,+∞)
B.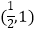
C.(1,3]
D.(1,5] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
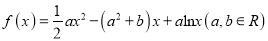
(Ⅰ)当
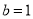 时,求函数
时,求函数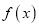 的单调区间;
的单调区间; (Ⅱ)当
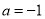 ,
,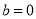 时,证明:
时,证明: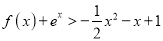 (其中
(其中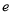 为自然对数的底数).
为自然对数的底数). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
:  的焦点
的焦点 与椭圆
与椭圆 :
:  的一个焦点重合,点
的一个焦点重合,点 在抛物线上,过焦点
在抛物线上,过焦点 的直线
的直线 交抛物线于
交抛物线于 、
、 两点.
两点. (Ⅰ)求抛物线
 的方程以及
的方程以及 的值;
的值;(Ⅱ)记抛物线的准线
 与
与 轴交于点
轴交于点 ,试问是否存在常数
,试问是否存在常数 ,使得
,使得 且
且 都成立?若存在,求出实数
都成立?若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=lnx,g(x)=
 +mx+
+mx+  (m<0),直线l与函数f(x)的图象相切,切点的横坐标为1,且直线l与函数g(x)的图象也相切.
(m<0),直线l与函数f(x)的图象相切,切点的横坐标为1,且直线l与函数g(x)的图象也相切.
(1)求直线l的方程及实数m的值;
(2)若h(x)=f(x+1)﹣g′(x)(其中g′(x)是g(x)的导函数),求函数h(x)的最大值;
(3)当0<b<a时,求证:f(a+b)﹣f(2a)< .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系
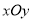 中,
中, 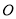 为坐标原点,曲线
为坐标原点,曲线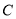 :
: 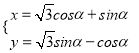 (
(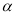 为参数),在以平面直角坐标系的原点为极点,
为参数),在以平面直角坐标系的原点为极点, 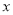 轴的正半轴为极轴,取相同单位长度的极坐标系,直线
轴的正半轴为极轴,取相同单位长度的极坐标系,直线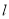 :
: 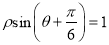 .
.(Ⅰ)求曲线
 的普通方程和直线
的普通方程和直线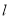 的直角坐标方程;
的直角坐标方程;(Ⅱ)曲线
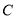 上恰好存在三个不同的点到直线
上恰好存在三个不同的点到直线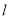 的距离相等,分别求出这三个点的极坐标.
的距离相等,分别求出这三个点的极坐标.
相关试题

