【题目】一盒中装有除颜色外其余均相同的12个小球,从中随机取出1个球,取出红球的概率为![]() ,取出黑球的概率为
,取出黑球的概率为![]() ,取出白球的概率为
,取出白球的概率为![]() ,取出绿球的概率为
,取出绿球的概率为![]() .求:
.求:
(1)取出的1个球是红球或黑球的概率;
(2)取出的1个球是红球或黑球或白球的概率.
参考答案:
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】试题分析:(1) 由互斥事件的概率公式得,取出1球是红球或黑球的概率为取出1球是红球的概率与取出1球是黑球的概率之和,(2) 由互斥事件的概率公式得,所求概率为取出1球是红球的概率、取出1球是黑球的概率与取出1球是白球的概率三者之和.
试题解析:记事件A1={任取1球为红球};A2={任取1球为黑球};
A3={任取1球为白球},A4={任取1球为绿球},
则P(A1)=![]() ,P(A2)=
,P(A2)=![]() ,P(A3)=
,P(A3)=![]() ,P(A4)=
,P(A4)=![]() .根据题意,知事件A1,A2,A3,A4彼此互斥.
.根据题意,知事件A1,A2,A3,A4彼此互斥.
由互斥事件的概率公式,得
(1)取出1球是红球或黑球的概率为P(A1∪A2)=P(A1)+P(A2)=![]() +
+![]() =
=![]() .
.
(2)取出1球是红球或黑球或白球的概率为P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3)=![]() +
+![]() +
+![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:存在实数m,使方程x2+mx+1=0有两个不等的负根;命题q:存在实数m,使方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第
 年需要付出设备的维修和工人工资等费用
年需要付出设备的维修和工人工资等费用 的信息如下图 .
的信息如下图 .
(1)求
 ;
;(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,在四面体PABC中,S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.写出对四面体性质的猜想,并证明你的结论


-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
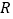 上的偶函数
上的偶函数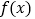 满足
满足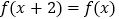 ,且在
,且在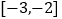 上是减函数,若
上是减函数,若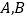 是锐角三角形
是锐角三角形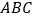 的两个内角,则下列各式一定成立的是( )
的两个内角,则下列各式一定成立的是( )A.
 B.
B. 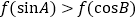
C.
 D.
D. 
相关试题

