【题目】已知命题p:存在实数m,使方程x2+mx+1=0有两个不等的负根;命题q:存在实数m,使方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求m的取值范围.
参考答案:
【答案】m≥3或1<m≤2.
【解析】
试题分析:利用一元二次方程的实数根与判别式的关系、不等式的解法可得命题P与Q的m的取值范围,再由“P或Q”为真,“P且Q”为假,可得P与Q必然一个为真一个为假.即可得出
试题解析:存在实数m,使方程x2+mx+1=0有两个不等的负根,则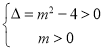 ,解得m>2,即m>2时,p真.
,解得m>2,即m>2时,p真.
存在实数m,使方程4x2+4(m-2)x+1=0无实根,
则Δ=16(m-2)2-16=16(m2-4m+3)<0,
解得1<m<3,即1<m<3时,q真.
因“p或q”为真,所以命题p、q至少有一个为真,
又“p且q”为假,所以命题p、q至少有一个为假,
因此,命题p、q应为一真一假,即命题p为真,命题q为假或命题p为假,命题q为真.
∴![]() 或
或![]() ,解得m≥3或1<m≤2.
,解得m≥3或1<m≤2.
所以m的取值范围是m≥3或1<m≤2
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
, .
.(Ⅰ)当
 ,
, 时,设
时,设 ,求证:对任意的
,求证:对任意的 ,
, ;
;(Ⅱ)当
 时,若对任意
时,若对任意 ,不等式
,不等式 恒成立.求实数
恒成立.求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.(1)求椭圆
 的方程;
的方程;(2)若
 是椭圆
是椭圆 的左顶点,经过左焦点
的左顶点,经过左焦点 的直线
的直线 与椭圆
与椭圆 交于
交于 ,
, 两点,求
两点,求 与
与 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.( 为坐标原点)
为坐标原点) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一盒中装有除颜色外其余均相同的12个小球,从中随机取出1个球,取出红球的概率为
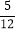 ,取出黑球的概率为
,取出黑球的概率为 ,取出白球的概率为
,取出白球的概率为 ,取出绿球的概率为
,取出绿球的概率为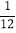 .求:
.求:(1)取出的1个球是红球或黑球的概率;
(2)取出的1个球是红球或黑球或白球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第
 年需要付出设备的维修和工人工资等费用
年需要付出设备的维修和工人工资等费用 的信息如下图 .
的信息如下图 .
(1)求
 ;
;(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
相关试题

