【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

参考答案:
【答案】(I)![]() (II)见解析.
(II)见解析.
【解析】试题分析:
(1)利用等体积法结合题意可求得![]() 到平面
到平面![]() 的距离为
的距离为![]() ;
;
(2)当![]() 时满足题意,利用题中所给的条件进行证明即可.
时满足题意,利用题中所给的条件进行证明即可.
试题解析:
解:(1)方法一:因为![]() 平面
平面![]() ,
, ![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() ,所以
,所以![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
方法二:等积法求高.
(2)解:在线段![]() 上存在一点
上存在一点![]() ,使
,使![]() 平面
平面![]() ,
,
下面给出证明:设![]() 为线段
为线段![]() 上的一点,且
上的一点,且![]() ,
,
过点![]() 作
作![]() 交于点
交于点![]() ,则
,则![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)是定义在R上的奇函数,且x<0时,f(x)=1+2x.
(1)求函数f(x)的解析式;
(2)画出函数f(x)的图像;
(3)写出函数f(x)的单调区间及值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员
 名,其中种子选手
名,其中种子选手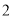 名;乙协会的运动员
名;乙协会的运动员 名,其中种子选手
名,其中种子选手 名.从这
名.从这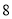 名运动员中随机选择
名运动员中随机选择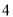 人参加比赛.
人参加比赛.(1)设
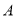 为事件“选出的
为事件“选出的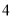 人中恰有
人中恰有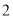 名种子选手,且这
名种子选手,且这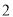 名种子选手来自同一个协会”求事件
名种子选手来自同一个协会”求事件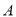 发生的概率;
发生的概率;(2)设
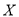 为选出的
为选出的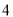 人中种子选手的人数,求随机变量
人中种子选手的人数,求随机变量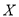 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
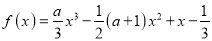 (
(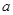
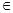 R).
R).(1) 若
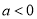 ,求函数
,求函数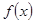 的极值;
的极值;(2)是否存在实数
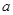 使得函数
使得函数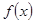 在区间
在区间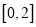 上有两个零点,若存在,求出
上有两个零点,若存在,求出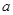 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】f(x)是定义在R上的奇函数,对x,y∈R都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,f(-1)=2.
(1)求证:f(x)为奇函数;
(2)求证:f(x)是R上的减函数;
(3)求f(x)在[-2,4]上的最值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直三棱柱
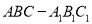 中,
中, 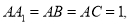
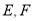 分别是
分别是 的中点, 且
的中点, 且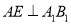 ,
,(1)证明:
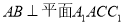 .
.(2)棱
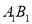 上是否存在一点
上是否存在一点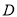 ,使得平面
,使得平面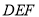 与平面
与平面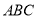 所成锐二面角的余弦值为
所成锐二面角的余弦值为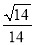 若存在,说明点
若存在,说明点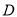 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.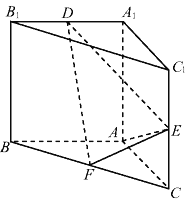
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=5x+x-2,g(x)=log5x+x-2的零点分别为x1,x2,则x1+x2的值为________.
相关试题

