【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且经过点
,且经过点![]() ,直线
,直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() .
.
(1)求椭圆的方程;
(2)求![]() 的取值范围;
的取值范围;
(3)若直线![]() 不过点
不过点![]() ,求证:直线
,求证:直线![]() 的斜率互为相反数.
的斜率互为相反数.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)设出椭圆方程的标准形式,由离心率的值及椭圆过点(4,1)求出待定系数,得到椭圆的标准方程;
(2)把直线方程代入椭圆的方程,由判别式大于0,求出m的范围;
(3)由方程联立可得到两根之和、两根之积,从而可求直线MA,MB斜率之和,化简可得结论.
(1) 设椭圆的方程为 ![]() ,因为
,因为 ![]() ,所以
,所以 ![]() ,
,
又因为 ![]() ,所以
,所以 ![]() ,解得
,解得 ![]() ,故椭圆方程为
,故椭圆方程为 ![]() .
.
(2) 将 y=x+m 代入 ![]() 并整理得
并整理得 ![]() ,
,![]() ,解得 -5<m<5.
,解得 -5<m<5.
(3) 设直线MA,MB 的斜率分别为 ![]() ,只要证明
,只要证明 ![]() ,
,
设 ![]() ,
,
则 ![]() ,
,![]() ,
,
![]() ,
,
分子![]()
![]()
![]()
所以直线 MA,MB 的斜率互为相反数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆N:x2+(y+
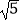 )2=36,P是圆N上的点,点Q在线段NP上,且有点D(0,
)2=36,P是圆N上的点,点Q在线段NP上,且有点D(0, 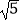 )和DP上的点M,满足
)和DP上的点M,满足 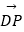 =2
=2 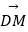 ,
, 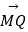
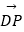 =0.
=0. 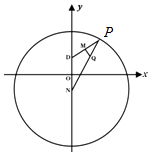
(1)当P在圆上运动时,求点Q的轨迹方程;
(2)若斜率为 的直线l与(1)中所求Q的轨迹交于不同两点A、B,又点C(
的直线l与(1)中所求Q的轨迹交于不同两点A、B,又点C(  ,2),求△ABC面积最大值时对应的直线l的方程.
,2),求△ABC面积最大值时对应的直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=(ax2+ax+x+a)e﹣x(a≤0).
(1)讨论y=f(x)的单调性;
(2)当a=0时,若f(x1)=f(x2) (x1≠x2),求证x1+x2>2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为6的等边三角形各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正三棱柱形的容器.

(1)若这个容器的底面边长为
 ,容积为
,容积为 ,写出
,写出 关于
关于 的函数关系式并注明定义域;
的函数关系式并注明定义域;(2)求这个容器容积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C的参数方程是
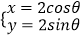 (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1,
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1, 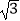 )
)
(1)求直线AB的直角坐标方程;
(2)在曲线C上求一点M,使点M到AB的距离最大,并求出些最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)当
 时,讨论函数
时,讨论函数 零点的个数;
零点的个数;(2)若
 ,当
,当 =1时,求证:
=1时,求证:
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小学庆“六一”晚会共由6个节目组成,演出顺序有如下要求:节目
 必须排在前两位,节目
必须排在前两位,节目 不能排在第一位,节目
不能排在第一位,节目 必须排在最后一位,该台晚会节目演出顺序的编排方案共有( )
必须排在最后一位,该台晚会节目演出顺序的编排方案共有( )A. 36种 B. 42种 C. 48种 D. 54种
相关试题

