【题目】已知函数![]()
(1)当![]() 时,讨论函数
时,讨论函数![]() 零点的个数;
零点的个数;
(2)若![]() ,当
,当![]() =1时,求证:
=1时,求证:![]()
参考答案:
【答案】(1) 当 ![]() 时,函数
时,函数![]() 有两个不同的零点;当
有两个不同的零点;当![]() 时,函数
时,函数![]() 有且仅有一个零点;当
有且仅有一个零点;当![]() , 函数
, 函数![]() 没有零点.
没有零点.
(2)证明见解析.
【解析】试题分析:(1)对![]() 进行化简,构造函数
进行化简,构造函数![]() ,研究函数h(x)的单调性和最值,即可确定F(x)=f(x)﹣xlnx在定义域内是否存在零点;(2)由(Ⅰ)知,当a=1时f(x)在(0,+∞)上单调递增,要证明f(g(x))<f(x),只要证明g(x)<x即可.
,研究函数h(x)的单调性和最值,即可确定F(x)=f(x)﹣xlnx在定义域内是否存在零点;(2)由(Ⅰ)知,当a=1时f(x)在(0,+∞)上单调递增,要证明f(g(x))<f(x),只要证明g(x)<x即可.
详解:
(1)函数![]() 的定义域为
的定义域为![]()
由 ![]() 得
得![]()
令![]() 则
则![]()
由于![]() ,可知当
,可知当 ![]() 当
当![]() 时
时![]()
故函数![]() 在(0,1)上单调递减,在
在(0,1)上单调递减,在![]() 上单调递增,
上单调递增,
故![]() ,又
,又![]()
当 ![]() 时,函数
时,函数![]() 有两个不同的零点;
有两个不同的零点;
当![]() 时,函数
时,函数![]() 有且仅有一个零点;
有且仅有一个零点;
当![]() , 函数
, 函数![]() 没有零点.
没有零点.
(2)函数定义域为![]() 时,
时,![]()
由 ![]() 得:
得:![]()
![]() 时,
时,![]() 在
在![]() 上单调递增,且
上单调递增,且![]() 故对任意
故对任意![]()
所以,要证明![]() ,只需证:
,只需证:![]()
只需证:![]()
即证:![]()
即证;![]()
所以,要证明;![]()
令 ![]() 则
则![]()
故函数![]() 在
在![]() 上单调递增;
上单调递增;![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为6的等边三角形各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正三棱柱形的容器.

(1)若这个容器的底面边长为
 ,容积为
,容积为 ,写出
,写出 关于
关于 的函数关系式并注明定义域;
的函数关系式并注明定义域;(2)求这个容器容积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆的中心在原点,焦点在
 轴上,离心率为
轴上,离心率为 ,且经过点
,且经过点 ,直线
,直线 交椭圆于不同的两点
交椭圆于不同的两点 .
.(1)求椭圆的方程;
(2)求
 的取值范围;
的取值范围;(3)若直线
 不过点
不过点 ,求证:直线
,求证:直线 的斜率互为相反数.
的斜率互为相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C的参数方程是
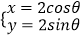 (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1,
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1, 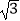 )
)
(1)求直线AB的直角坐标方程;
(2)在曲线C上求一点M,使点M到AB的距离最大,并求出些最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某小学庆“六一”晚会共由6个节目组成,演出顺序有如下要求:节目
 必须排在前两位,节目
必须排在前两位,节目 不能排在第一位,节目
不能排在第一位,节目 必须排在最后一位,该台晚会节目演出顺序的编排方案共有( )
必须排在最后一位,该台晚会节目演出顺序的编排方案共有( )A. 36种 B. 42种 C. 48种 D. 54种
-
科目: 来源: 题型:
查看答案和解析>>【题目】在独立性检验中,统计量
 有三个临界值:2.706,3.841和6.635.当
有三个临界值:2.706,3.841和6.635.当 时,有90%的把握说明两个事件有关;当
时,有90%的把握说明两个事件有关;当 时,有95%的把握说明两个事件有关,当
时,有95%的把握说明两个事件有关,当 时,有99%的把握说明两个事件有关,当
时,有99%的把握说明两个事件有关,当 时,认为两个事件无关.在一项打鼾与心脏病的调查中,共调查了2000人,经计算
时,认为两个事件无关.在一项打鼾与心脏病的调查中,共调查了2000人,经计算 .根据这一数据分析,认为打鼾与患心脏病之间( )
.根据这一数据分析,认为打鼾与患心脏病之间( )A. 有95%的把握认为两者有关 B. 约95%的打鼾者患心脏病
C. 有99%的把握认为两者有关 D. 约99%的打鼾者患心脏病
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣1|+|x﹣a|.
(1)若a=﹣1,解不等式f(x)≥3;
(2)如果x∈R,使得f(x)<2成立,求实数a的取值范围.
相关试题

