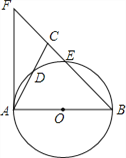
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若![]() ,CE∶EB=1∶4,求CE的长.
,CE∶EB=1∶4,求CE的长.
参考答案:
【答案】(1)见解析;(2)2。
【解析】试题分析:(1)依据题设条件证明“∠CAF=∠ABD”,即说明BA=BC,再借助等腰三角形的高线即为角平分线进行推证;(2)借助相似三角形的性质,即对应边成比例建立方程进行求解:
解: (1) 证明:连接BD.
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°.
∵AF是⊙O的切线,
∴∠FAB=90°,
∴∠CAF+∠DAB=90°,
∴∠CAF=∠ABD,
∴BA=BC
∴∠ABC=2∠ABD
∴∠ABC=2∠CAF.
(2)解:连接DE,
∵四边形ABED是圆内接四边形,
∴∠ABC=∠CDE,∠CED=∠CAB,
∴△CDE∽△CBA,
∴CD∶CB=CE∶CA
∴CD×CA=CE×CB
∴BA=BC,∠ADB=90°
∴![]()
设CE=x,∵CE:EB=1:4,∴EB=5x,
∴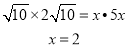
∴CE=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出
 与销售额
与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据: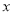
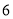
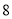
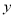
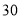
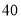
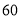
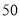
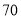
(1)求回归直线方程;
(2)试预测广告费支出为
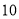 万元时,销售额多大?
万元时,销售额多大?(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过
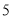 的概率.(参考数据:
的概率.(参考数据: 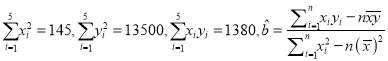 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=
 ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积 -
科目: 来源: 题型:
查看答案和解析>>【题目】一盒中放有的黑球和白球,其中黑球4个,白球5个.
(1)从盒中同时摸出两个球,求两球颜色恰好相同的概率.
(2)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
(3)从盒中不放回的每次摸一球,若取到白球则停止摸球,求取到第三次时停止摸球的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各2张,让孩子从盒子里任取3张卡片,按卡片上最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字
(1)求取出的3张卡片上的数字互不相同的概率;
(2)求随机变量x的分布列;
(3)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍。设购进A掀电脑x台,这100台电脑的销售总利润为y元。
①求y与x的关系式;
②该商店购进A型、B型各多少台,才能使销售利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台。若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
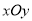 中,曲线
中,曲线 的参数方程为
的参数方程为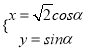 (
(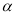 为参数),以原点
为参数),以原点 为极点,
为极点, 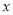 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线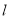 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
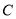 的普通方程与直线
的普通方程与直线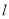 的直角坐标方程;
的直角坐标方程;(2)设
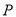 为曲线
为曲线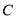 上的动点,求点
上的动点,求点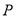 的直线
的直线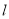 的距离的最小值.
的距离的最小值.
相关试题

