【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式,并画出的f(x)图象; 
(2)设g(x)=f(x)﹣k,利用图象讨论:当实数k为何值时,函数g(x)有一个零点?二个零点?三个零点?
参考答案:
【答案】
(1)解:当x≥0时,f(x)=x2﹣2x.
设x<0可得﹣x>0,则f(﹣x)=(﹣x)2﹣2(﹣x)=x2+2x
∵函数f(x)为奇函数,则f(x)=﹣f(﹣x)=﹣x2﹣2x
∴ ![]() 函数的图象如图所示
函数的图象如图所示
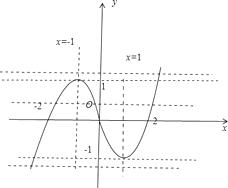
(2)解:由g(x)=f(x)﹣k=0可得f(x)=k
结合函数的图象可知
①当k<﹣1或k>1时,y=k与y=f(x)的图象有1个交点,即g(x)=f(x)﹣k有1个零点
②当k=﹣1或k=1时,y=k与y=f(x)有2个交点,即g(x)=f(x)﹣k有2个零点
③当﹣1<k<1时,y=k与y=f(x)有3个交点,即g(x)=f(x)﹣k有3个零点
【解析】(1)先设x<0可得﹣x>0,则f(﹣x)=(﹣x)2﹣2(﹣x)=x2+2x,由函数f(x)为奇函数可得f(x)=﹣f(﹣x),可求,结合二次函数的图象可作出f(x)的图象;(2)由g(x)=f(x)﹣k=0可得f(x)=k,结合函数的图象可,要求g(x)=f(x)﹣k的零点个数,只要结合函数的图象,判断y=f(x)与y=k的交点个数
【考点精析】利用函数奇偶性的性质对题目进行判断即可得到答案,需要熟知在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
2
3
4
5
6
y
2.2
3.8
5.5
6.5
7.0
若由资料知,y对x呈线性相关关系,试求:
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,求出y关于x的线性回归方程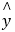 =bx+
=bx+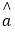 ;
;
(Ⅲ)估计使用年限为10年时,维修费用约是多少?
(参考数据:2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x﹣2﹣x .
(1)判断函数f(x)的奇偶性;
(2)证明:函数f(x)为(﹣∞,+∞)上的增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数满足f(x+1)﹣f(x)=2x且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[﹣1,1]上不等式f(x)>2x+m恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组中的函数f(x)与g(x),是同一函数的是( )
A.f(x)=ln(1﹣x)+ln(1+x),g(x)=ln(1﹣x2)
B.f(x)=lgx2 , g(x)=2lgx
C.f(x)=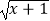 ?
? 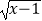 ,g(x)=
,g(x)= 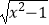
D.f(x)=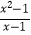 ,g(x)=x+1
,g(x)=x+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数据
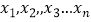 是上海普通职工n
是上海普通职工n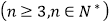 个人的年收入,设n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入
个人的年收入,设n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入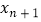 , 则这n+1个数据中,下列说法正确的是 ( )
, 则这n+1个数据中,下列说法正确的是 ( )
A.年收入平均数大大增加,中位数一定变大,方差可能不变
B.年收入平均数大大增加,中位数可能不变,方差变大
C.年收入平均数大大增加,中位数可能不变,方差也不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=logax,y=logbx,y=logcx,y=logdx的图象如图所示,则a,b,c,d的大小顺序是( )
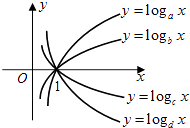
A.1<d<c<a<b
B.c<d<1<a<b
C.c<d<1<b<a
D.d<c<1<a<b
相关试题

