【题目】假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
2 | 3 | 4 | 5 | 6 | |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系,试求:
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,求出y关于x的线性回归方程![]() =bx+
=bx+![]() ;
;
(Ⅲ)估计使用年限为10年时,维修费用约是多少?
(参考数据:2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3)
参考答案:
【答案】解:(I)表中数据的散点图如下图所示:
(II)∵b=![]() =1.23
=1.23
∵![]() =4,
=4,![]() =5,
=5,
∴样本中心点的坐标是(4,5)
∴5=4×1.23+a
∴a=0.08,
∴线性回归方程是y=1.23x+0.08,
(III)当x=10时,y=1.23×10+0.08=12.38
∴使用年限为10年时,维修费用约是12.38万元
【解析】(I)由已知中某设备使用年限x(年)和所支出的维修费用y(万元)的统计表中数据,易画出数据的散点图;
(Ⅱ)根据所给的样本中心点和两个最小二乘法要用的和式,写出b的表示式,求出结果,再代入样本中心点求出a,写出线性回归方程;
(III)根据(II)中所得的线性回归方程,代入x=10求出预报值,即使用年限为10年时,维修费用的估算值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=ax(a>0,a≠1)在[﹣1,2]上的最大值为4,最小值为m,且函数g(x)=(1﹣4m)
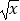 在[0,+∞)上是增函数,则m= , a= .
在[0,+∞)上是增函数,则m= , a= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x)在(0,+∞)内是减函数,又有f(3)=0,则f(x)>0的解集为 , xf(x)<0的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂的某产品产量与单位成本的资料如表所示:
产量x千件
2
4
5
6
8
单位成本y元/件
30
40
60
50
70
请画出散点图并从图中判断产品产量与单位成本成什么样的关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x﹣2﹣x .
(1)判断函数f(x)的奇偶性;
(2)证明:函数f(x)为(﹣∞,+∞)上的增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数满足f(x+1)﹣f(x)=2x且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[﹣1,1]上不等式f(x)>2x+m恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式,并画出的f(x)图象;
(2)设g(x)=f(x)﹣k,利用图象讨论:当实数k为何值时,函数g(x)有一个零点?二个零点?三个零点?
相关试题

