搜索
【题目】已知函数f（x）=2x﹣2﹣x ．
（1）判断函数f（x）的奇偶性；
（2）证明：函数f（x）为（﹣∞，+∞）上的增函数．
参考答案：
【答案】
（1）解：函数f（x）的定义域是R，
因为f（﹣x）=2﹣x﹣2x=﹣（2x﹣2﹣x）=﹣f（x），
所以函数f（x）=2x﹣2﹣x是奇函数
（2）解：设x1＜x2，
则f（x1）=2 
﹣2 
，f（x2）=2 
﹣2 
，
∴f（x1）﹣f（x2）=2 ﹣2 ﹣（2 ﹣2 ）
= 
，
∵x1＜x2，
∴ 
，1+ 
＞0，
∴f（x1）＜f（x2），
∴函数f（x）为（﹣∞，+∞）上的增函数
【解析】（1）首先明确函数的定义域为R，然后利用奇偶函数的定义判断．（2）根据增函数的定义进行证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果定义在（﹣∞，0）∪（0，+∞）上的奇函数f（x）在（0，+∞）内是减函数，又有f（3）=0，则f（x）＞0的解集为 ， xf（x）＜0的解集为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂的某产品产量与单位成本的资料如表所示：
产量x千件
2
4
5
6
8
单位成本y元/件
30
40
60
50
70
请画出散点图并从图中判断产品产量与单位成本成什么样的关系？
-
科目： 来源： 题型：
查看答案和解析>>【题目】假设关于某设备使用年限x（年）和所支出的维修费用y（万元）有如下统计资料：
2
3
4
5
6
y
2.2
3.8
5.5
6.5
7.0
若由资料知，y对x呈线性相关关系，试求：
（Ⅰ）请画出上表数据的散点图；
（Ⅱ）请根据上表提供的数据，求出y关于x的线性回归方程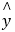
=bx+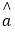
；
（Ⅲ）估计使用年限为10年时，维修费用约是多少？
（参考数据：2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3） -
科目： 来源： 题型：
查看答案和解析>>【题目】若二次函数满足f（x+1）﹣f（x）=2x且f（0）=1．
（1）求f（x）的解析式；
（2）若在区间[﹣1，1]上不等式f（x）＞2x+m恒成立，求实数m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2﹣2x．
（1）求f（x）的解析式，并画出的f（x）图象；
（2）设g（x）=f（x）﹣k，利用图象讨论：当实数k为何值时，函数g（x）有一个零点？二个零点？三个零点？ -
科目： 来源： 题型：
查看答案和解析>>【题目】下列四组中的函数f（x）与g（x），是同一函数的是（ ）
A.f（x）=ln（1﹣x）+ln（1+x），g（x）=ln（1﹣x2）
B.f（x）=lgx2 ， g（x）=2lgx
C.f（x）=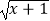
? 
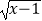，g（x）=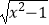 
D.f（x）=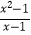
，g（x）=x+1
相关试题
