【题目】已知数列{an}满足:an≠0,a1= ![]() ,an﹣an+1=2anan+1 . (n∈N*).
,an﹣an+1=2anan+1 . (n∈N*).
(1)求证:{ ![]() }是等差数列,并求出an;
}是等差数列,并求出an;
(2)证明:a1a2+a2a3+…+anan+1< ![]() .
.
参考答案:
【答案】
(1)证明:a1= ![]() ,an﹣an+1=2anan+1.可得
,an﹣an+1=2anan+1.可得
![]() ﹣
﹣ ![]() =2,则{
=2,则{ ![]() }是首项为3,公差为2的等差数列,
}是首项为3,公差为2的等差数列,
![]() =
= ![]() +2(n﹣1)=3+2(n﹣1)=2n+1,
+2(n﹣1)=3+2(n﹣1)=2n+1,
即有an= ![]()
(2)证明:a1a2+a2a3+…+anan+1= ![]() +
+ ![]() +…+
+…+ ![]()
= ![]() (
( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
= ![]() (
( ![]() ﹣
﹣ ![]() )=
)= ![]() ﹣
﹣ ![]()
![]() <
< ![]()
【解析】(1)两边除以anan+1 , 由等差数列的定义和通项公式,即可得证,由等差数列的通项公式即可得到;(2)运用数列的求和方法:裂项相消求和,运用不等式的性质,即可得证.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱
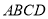 与四边形
与四边形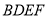 相交于
相交于 ,
, 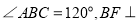 平面
平面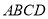 ,
, 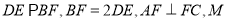 为
为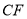 的中点,
的中点, 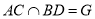 .
.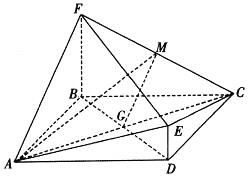
(I)求证:
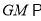 平面
平面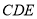 ;
; (II)求直线
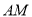 与平面
与平面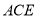 成角的正弦值.
成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在区间[﹣1,1]上任取两个数a,b,在下列条件时,分别求不等式x2+2ax+b2≥0恒成立时的概率:
(1)当a,b均为整数时;
(2)当a,b均为实数时. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
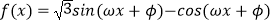 (0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为  .
.
(1)求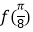 的值;
的值;
(2)将函数y=f(x)的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,A=60°,a=3.
(1)若b=2,求cosB;
(2)求△ABC的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,A(1,1),B(2,0),|
 |=1.
|=1.
(1)求 与
与  夹角;
夹角;
(2)若 与
与  垂直,求点C的坐标;
垂直,求点C的坐标;
(3)求| +
+  +
+  |的取值范围.
|的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 .
.(Ⅰ)若
 在
在 上单调递减,求
上单调递减,求 的取值范围;
的取值范围;(Ⅱ)讨论
 的单调性.
的单调性.
相关试题

