【题目】已知函数 ![]() (0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)将函数y=f(x)的图象向右平移 ![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
参考答案:
【答案】
(1)解: ![]() =
= ![]() =
= ![]() .
.
∵f(x)为偶函数,
∴对x∈R,f(﹣x)=f(x)恒成立,
∴ ![]() .
.
即 ![]() ,
,
整理得 ![]() .
.
∵ω>0,且x∈R,所以 ![]() .
.
又∵0<φ<π,故 ![]() .
.
∴ ![]() .
.
由题意得 ![]() ,所以ω=2.
,所以ω=2.
故f(x)=2cos2x.
∴ ![]() .
.
(2)解:将f(x)的图象向右平移 ![]() 个单位后,得到
个单位后,得到 ![]() 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到
的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到 ![]() 的图象.
的图象.
∴ ![]() .
.
当 ![]() (k∈Z),
(k∈Z),
即 ![]() (k∈Z)时,g(x)单调递减,
(k∈Z)时,g(x)单调递减,
因此g(x)的单调递减区间为 ![]() (k∈Z)
(k∈Z)
【解析】(1)先用两角和公式对函数f(x)的表达式化简得f(x)=2sin(ωx+φ﹣ ![]() ),利用偶函数的性质即f(x)=f(﹣x)求得ω,进而求出f(x)的表达式,把x=
),利用偶函数的性质即f(x)=f(﹣x)求得ω,进而求出f(x)的表达式,把x= ![]() 代入即可.(2)根据三角函数图象的变化可得函数g(x)的解析式,再根据余弦函数的单调性求得函数g(x)的单调区间.
代入即可.(2)根据三角函数图象的变化可得函数g(x)的解析式,再根据余弦函数的单调性求得函数g(x)的单调区间.
【考点精析】本题主要考查了两角和与差的正弦公式和函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握两角和与差的正弦公式:![]() ;图象上所有点向左(右)平移
;图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接珠海作为全国文明城市的复查,爱卫会随机抽取了60位路人进行问卷调查,调查项目是自己对珠海各方面卫生情况的满意度(假设被问卷的路人回答是客观的),以分数表示问卷结果,并统计他们的问卷分数,把其中不低于50分的分成五段[50,60),[60,70),…[90,100]后画出如图部分频率分布直方图,观察图形信息,回答下列问题:
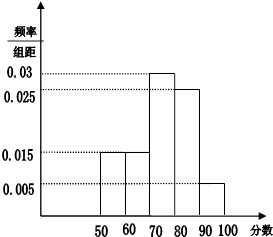
(1)求出问卷调查分数低于50分的被问卷人数;
(2)估计全市市民满意度在60分及以上的百分比. -
科目: 来源: 题型:
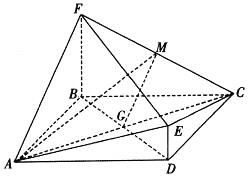
查看答案和解析>>【题目】如图,菱
 与四边形
与四边形 相交于
相交于 ,
, 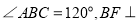 平面
平面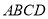 ,
, 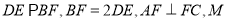 为
为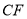 的中点,
的中点, 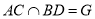 .
.
(I)求证:
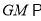 平面
平面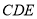 ;
; (II)求直线
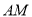 与平面
与平面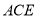 成角的正弦值.
成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在区间[﹣1,1]上任取两个数a,b,在下列条件时,分别求不等式x2+2ax+b2≥0恒成立时的概率:
(1)当a,b均为整数时;
(2)当a,b均为实数时. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足:an≠0,a1=
 ,an﹣an+1=2anan+1 . (n∈N*).
,an﹣an+1=2anan+1 . (n∈N*).
(1)求证:{ }是等差数列,并求出an;
}是等差数列,并求出an;
(2)证明:a1a2+a2a3+…+anan+1< .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,A=60°,a=3.
(1)若b=2,求cosB;
(2)求△ABC的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,A(1,1),B(2,0),|
 |=1.
|=1.
(1)求 与
与  夹角;
夹角;
(2)若 与
与  垂直,求点C的坐标;
垂直,求点C的坐标;
(3)求| +
+  +
+  |的取值范围.
|的取值范围.
相关试题

