【题目】已知函数f(x)=lnx,g(x)= ![]() x2﹣kx;
x2﹣kx;
(1)设k=m+ ![]() (m>0),若函数h(x)=f(x)+g(x)在区间(0,2)内有且仅有一个极值点,求实数m的取值范围;
(m>0),若函数h(x)=f(x)+g(x)在区间(0,2)内有且仅有一个极值点,求实数m的取值范围;
(2)设M(x)=f(x)﹣g(x),若函数M(x)存在两个零点x1 , x2(x1>x2),且满足2x0=x1+x2 , 问:函数M(x)在(x0 , M(x0))处的切线能否平行于直线y=1,若能,求出该切线方程,若不能,请说明理由.
参考答案:
【答案】
(1)解:因为h(x)=lnx+ ![]() x2﹣kx;
x2﹣kx;
h′(x)= ![]() +x﹣k,
+x﹣k,
由题意可得:k≥ ![]() ,
,
m+ ![]() =k≥
=k≥ ![]() ,
,
可得0<m≤ ![]() 或m≥2,
或m≥2,
综上,m的取值范围为{m丨0<m≤ ![]() 或m≥2}
或m≥2}
(2)解:假设,函数M(x)在(x0,M(x0))处的切线平行于直线y=1,
M(x)=f(x)﹣g(x)=lnx﹣ ![]() x2+kx,M′(x)=f(x)﹣g(x)=
x2+kx,M′(x)=f(x)﹣g(x)= ![]() ﹣x+k,
﹣x+k,
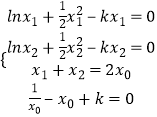 ,
,
由ln ![]() ﹣
﹣ ![]() (x1+x2)(x1﹣x2)=﹣k(x1﹣x2),
(x1+x2)(x1﹣x2)=﹣k(x1﹣x2),
∴﹣k= ![]() ﹣x0,结合
﹣x0,结合 ![]() ,
,
可得:ln ![]() =
= ![]() =
=  ,
,
令u= ![]() ∈(0,1),
∈(0,1),
∴lnu﹣ ![]() =0,u∈(0,1),
=0,u∈(0,1),
设y=lnu﹣ ![]() ,u∈(0,1),
,u∈(0,1),
y′= ![]() +
+ ![]() =
= ![]() =
= ![]() >0,
>0,
所以函数y=lnu﹣ ![]() ,在(0,1)上单调递增,
,在(0,1)上单调递增,
因此,y<0,即lnu﹣ ![]() <0,也就是ln
<0,也就是ln ![]() <
<  ,此时与ln
,此时与ln ![]() =
=  矛盾,所以数M(x)在(x0,M(x0))处的切线不能平行于直线y=1
矛盾,所以数M(x)在(x0,M(x0))处的切线不能平行于直线y=1
【解析】(1)求得h(x)及h′(x),由题意可知k≥ ![]() ,及k=m+
,及k=m+ ![]() 求得m的取值范围;(2)求得M(x)及M′(x),采用反证法,假设,函数M(x)在(x0 , M(x0))处的切线平行于直线y=1,根据题意列出方程,求得k的解析式,构造辅助函数,利用导数求得函数的单调性及最值,判断与已知是否相符,即可验证是否存在函数M(x)在(x0 , M(x0))处的切线平行于直线y=1,
求得m的取值范围;(2)求得M(x)及M′(x),采用反证法,假设,函数M(x)在(x0 , M(x0))处的切线平行于直线y=1,根据题意列出方程,求得k的解析式,构造辅助函数,利用导数求得函数的单调性及最值,判断与已知是否相符,即可验证是否存在函数M(x)在(x0 , M(x0))处的切线平行于直线y=1,
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌汽车4S店,对该品牌旗下的A型、B型、C型汽车进行维修保养,每辆车一年内需要维修的人工费用为200元,汽车4S店记录了该品牌三种类型汽车各100辆到店维修的情况,整理得下表:
车型
A型
B型
C型
频数
20
40
40
假设该店采用分层抽样的方法从上维修的100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访.
(1)从参加问卷到访的10辆汽车中随机抽取两辆,求这两辆汽车来自同一类型的概率;
(2)某公司一次性购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年维修人工费用总和,求ξ的分布列及数学期望(各型汽车维修的概率视为其需要维修的概率);
(3)经调查,该品牌A型汽车的价格与每月的销售量之间有如下关系:价格(万元)
25
23.5
22
20.5
销售量(辆)
30
33
36
39
已知A型汽车的购买量y与价格x符合如下线性回归方程:
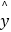 =
= 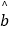 x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少?
x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】己知圆
 的圆心在直线
的圆心在直线 上,且过点
上,且过点 ,与直线
,与直线 相切.
相切.(
 )求圆
)求圆 的方程.
的方程.(
 )设直线
)设直线 与圆
与圆 相交于
相交于 ,
, 两点.求实数
两点.求实数 的取值范围.
的取值范围.(
 )在(
)在( )的条件下,是否存在实数
)的条件下,是否存在实数 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,F是椭圆P:
 (a>b>0)的右焦点,已知A(0,﹣2)与椭圆左顶点关于直线y=x对称,且直线AF的斜率为
(a>b>0)的右焦点,已知A(0,﹣2)与椭圆左顶点关于直线y=x对称,且直线AF的斜率为 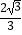 ,
,
(1)求椭圆P的方程;
(2)过点Q(﹣1,0)的直线l交椭圆P于M、N两点,交直线x=﹣4于点E, =
=  ,
,  =
=  ,证明:λ+μ为定值.
,证明:λ+μ为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,

(1)求证:BD=DE;
(2)若∠ECA=45°,求AP2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴,建立极坐标系,已知曲线C的参数方程是
 (θ为参数),曲线C与l的交点的极坐标为(2,
(θ为参数),曲线C与l的交点的极坐标为(2,  )和(2,
)和(2,  ),
),
(1)求直线l的普通方程;
(2)设P点为曲线C上的任意一点,求P点到直线l的距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(
 )已知三个点
)已知三个点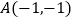 ,
,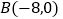 ,
,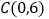 ,圆
,圆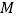 为
为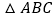 的外接圆.
的外接圆.(
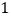 )求圆
)求圆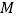 的方程.
的方程.(
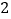 )设直线
)设直线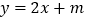 ,与圆
,与圆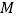 交于
交于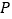 ,
,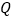 两点,且
两点,且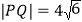 ,求
,求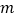 的值.
的值.
相关试题

