《2025年人教金学典同步练习册同步解析与测评高中物理必修第一册人教版》

例题 1 长 $ 100 \, m $ 的列车匀加速通过长 $ 1000 \, m $ 的隧道，列车刚进隧道时的速度是 $ 10 \, m/s $，完全出隧道时的速度是 $ 12 \, m/s $。根据以上条件回答下列问题。
(1) 列车通过隧道时的加速度是多少？
(2) 通过隧道所用时间是多少？

答案： 分析 题目中已知速度和位移，可以利用匀变速直线运动的速度和位移关系来求解，注意列车的长度不可忽略。列车的位移大小为 $ 1100 \, m $，而不是 $ 1000 \, m $。
解
(1) 求列车的加速度时，因为已经知道初速度、末速度和位移，所以可以根据公式 $ v^2 - v_0^2 = 2ax $ 求加速度，即 $ a = \frac{v^2 - v_0^2}{2x} = \frac{12^2 - 10^2}{2 × 1100} \, m/s^2 = 0.02 \, m/s^2 $。
(2) 通过隧道所用时间为 $ t = \frac{v - v_0}{a} = \frac{12 - 10}{0.02} \, s = 100 \, s $。

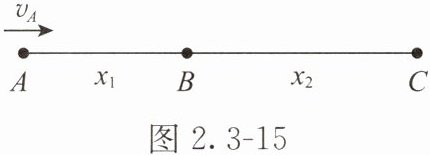
例题 2 有一个做匀变速直线运动的质点，它在两段连续相等的时间内通过的位移分别为 $ x_1 = 24 \, m $ 和 $ x_2 = 64 \, m $，如图 2.3 - 15 所示，连续相等的时间为 $ t = 4 \, s $，求质点的初速度 $ v_A $ 和加速度 $ a $ 的大小。

答案： 分析 匀变速直线运动的所有推论都是在基本公式上推理得到的，灵活利用各种推论能使解题过程简化。
解 解法 1 由匀变速直线运动公式求解。
两段连续相等的时间 $ t = 4 \, s $，通过的位移分别为 $ x_1 = 24 \, m $， $ x_2 = 64 \, m $。题中涉及位移和时间，故对前一过程和整个过程分别应用位移公式
$ x_1 = v_A t + \frac{1}{2}at^2 $
$ x_1 + x_2 = v_A(2t) + \frac{1}{2}a(2t)^2 $
由以上两式解得质点的加速度 $ a = \frac{x_2 - x_1}{t^2} = \frac{64 - 24}{4^2} \, m/s^2 = 2.5 \, m/s^2 $
再由公式 $ x_1 = v_A t + \frac{1}{2}at^2 $ 得 $ v_A = 1 \, m/s $。
解法 2 利用推论 $ \Delta x = aT^2 $ 求解。
由题意， $ T = t $，公式 $ \Delta x = at^2 $，则 $ a = \frac{\Delta x}{t^2} = \frac{x_2 - x_1}{t^2} = \frac{64 - 24}{4^2} \, m/s^2 = 2.5 \, m/s^2 $
再由公式 $ x_1 = v_A t + \frac{1}{2}at^2 $ 得 $ v_A = 1 \, m/s $。