《2025年自主学习能力测评四年级数学上册人教版》

4 解决问题。
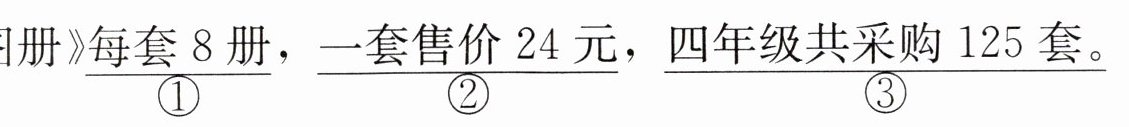
《少年儿童图册》$\underset{①}{\underline{每套8册}}$，$\underset{②}{\underline{一套售价24元}}$，$\underset{③}{\underline{四年级共采购125套}}$。
(1)每册《少年儿童图册》多少元？
解决这个问题需要用到的条件：①②。(填序号)
列式计算：
(2)这次采购一共花多少元？
解决这个问题需要用到的条件：②③。(填序号)
列式计算：
(3)解决上面两个问题时，都用到的已知条件：②。(填序号)
在解决问题(1)时，这个条件表示(总价)(填“单价”或“总价”)，在解决问题(2)时，这个条件表示(单价)(填“单价”或“总价”)。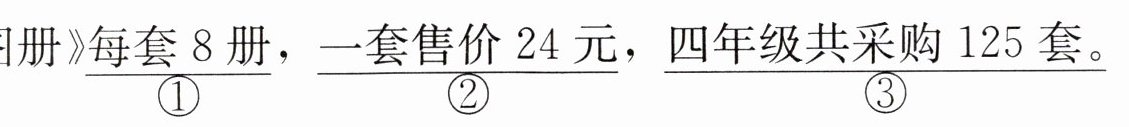

答案： 4.
(1) ①② 24÷8=3（元）
(2) ②③ 24×125=3000（元）
(3) ② 总价 单价

5 根据信息设计问题，并列式解答。

我设计的问题：每包巧克力多少钱？。
我会列式计算：54÷3=18（元）。

答案： 5. 答案不唯一，例如：每包巧克力多少钱？ 54÷3=18（元）

6 芒果品种繁多，不同品种的芒果售价也不一样。水果店有两种芒果，A品种每千克16元，B品种每千克10元。原计划买5千克A品种的钱，如果都换成买B品种，能买多少千克？

答案： 6. 16×5÷10=8（千克）