《2025年学能评价八年级数学上册浙教版》

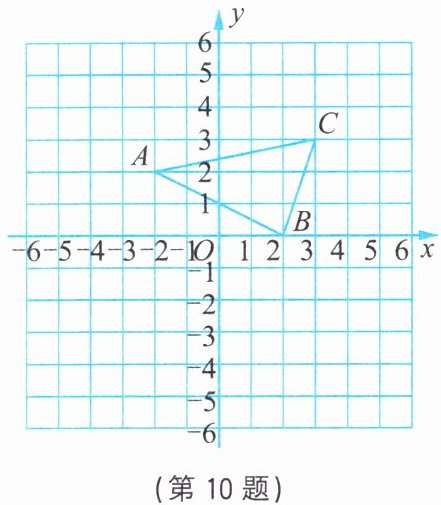
10. 如图，在平面直角坐标系中，已知$A(-2,2)$，$B(2,0)$，$C(3,3)$，$P(a,b)$是$\triangle ABC$的边 AC 上的一点，把$\triangle ABC$经过平移后得$\triangle DEF$，点 P 的对应点为$P^{\prime}(a - 2,b - 4)$。
(1) 写出 D，E，F 三点的坐标。
(2) 画出$\triangle DEF$。
(3) 求$\triangle DEF$的面积。

答案：
10.
(1)D(-4,-2),E(0,-4),F(1,-1)。
(2)如图所示:△DEF即为所求;
　　　　　 　　　　　
(3)作AM⊥x轴,CN⊥x轴,如图所示:
　　　　由已知可得:AM = 2,MN = 5,CN = 3,BM = 4,BN = 1。
　　　　因为△DEF由△ABC平移而来,所以S△DEF = S△ABC = S梯AMNC - S△AMB - S△CNB,
　　　　即S△DEF = $\frac{1}{2}$·(AM + CN)·MN - $\frac{1}{2}$·AM·MB - $\frac{1}{2}$·BN·CN
　　　　= $\frac{1}{2}$×(2 + 3)×5 - $\frac{1}{2}$×2×4 - $\frac{1}{2}$×1×3 = 7。

11. 在平面直角坐标系中，将点$A(m,n)$先向右平移 2 个单位，再向上平移 3 个单位，得到点$A^{\prime}$，若点$A^{\prime}$位于第二象限，则 m，n 的取值范围分别是(D)。

A.$m＜2$，$n＞3$
B.$m＜2$，$n＞-3$
C.$m＜-2$，$n＜-3$
D.$m＜-2$，$n＞-3$

答案： 11.D

12. 如图，在直角坐标系中，第一次将$\triangle OAB$变换成$\triangle OA_{1}B_{1}$，第二次将$\triangle OA_{1}B_{1}$变换成$\triangle OA_{2}B_{2}$，第三次将$\triangle OA_{2}B_{2}$变换成$\triangle OA_{3}B_{3}$。

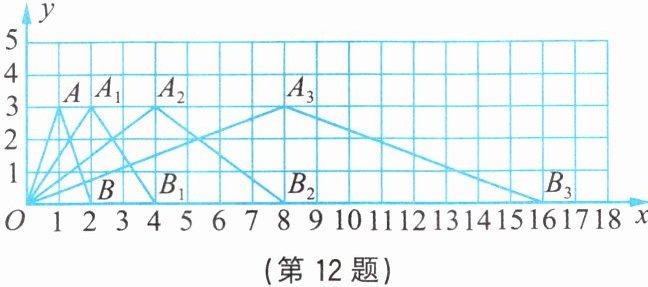
(1) 观察每次变换前后三角形的变化规律，按此变化规律，将$\triangle OA_{3}B_{3}$变换成$\triangle OA_{4}B_{4}$，则$A_{4}$的坐标是(16,3)，$B_{4}$的坐标是(32,0)。
(2) 按第(1)题找到的规律，将$\triangle OAB$进行 n 次变换，得到$\triangle OA_{n}B_{n}$。
①推测$A_{n}$的坐标是(2ⁿ,3)，$B_{n}$的坐标是(2ⁿ⁺¹,0)。
②求$\triangle OA_{n}B_{n}$的面积$S$。

答案： 12.
(1)每次变换后，点A,A₁,A₂,A₃的纵坐标不变，为3,同时横坐标都和2有关，为1,2,4,8，可表示为2ⁿ，那么A₄的坐标为(16,3);而点B,B₁,B₂,B₃的纵坐标不变，为0,同时横坐标都和2有关，为2ⁿ⁺¹，那么B₄的坐标为(32,0)。
(2)①由上题所得规律可知，Aₙ的纵坐标总为3,横坐标为2ⁿ，Bₙ的纵坐标总为0,横坐标为2ⁿ⁺¹，所以Aₙ的坐标是(2ⁿ,3),Bₙ的坐标是(2ⁿ⁺¹,0)。
②S = $\frac{1}{2}$×OBₙ×3 = $\frac{1}{2}$×2ⁿ⁺¹×3 = 3×2ⁿ。