《2025年练习与测试六年级数学上册苏教版彩色版》

1. 在括号里填合适的体积或容积单位。
(1) 一块橡皮的体积大约是 10(立方厘米)。
(2) 一个热水瓶大约能盛水 2(升)。
(3) 一部手机的体积大约是 50(立方厘米)。
(4) 教室的容积大约是 190(立方米)。

答案： 1.
(1)立方厘米
(2)升
(3)立方厘米
(4)立方米

2. 把一根长 12 分米的铁丝剪断后做成一个正方体框架，在框架的外面糊上彩纸，做成一个正方体模型。这个正方体模型的棱长是(1)分米，表面积是(6)平方分米，体积是(1)立方分米。

答案： 2.1，6，1

3. 用 12 个 1 立方厘米的小正方体摆成一个长方体，有多少种不同的摆法？在下表中填一填。(假设长≥宽≥高)

答案： 3*.长方体的长、宽、高可能是12厘米、1厘米、1厘米，可能是6厘米、2厘米、1厘米，可能是4厘米、3厘米、1厘米，可能是3厘米、2厘米、2厘米，体积都是12立方厘米。

做一做
下面的立体图形都是由若干个多边形围成的，它们都是多面体。

数出每个多面体的顶点数、棱数和面数，并填表。

观察上表，想一想：多面体的顶点数、棱数、面数之间有什么关系？如果用字母 V 表示顶点的个数，E 表示棱的条数，F 表示面的个数，这一规律可以怎样表示？
V+F-E=2
表示多面体顶点数、棱数、面数之间关系的公式叫作欧拉公式，是瑞士数学家欧拉最早发现的。

答案：
做一做.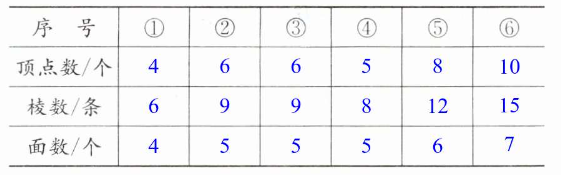，规律：V+F-E=2。