《2025年小学生学习指导丛书三年级数学上册人教版》

单元知识结构图

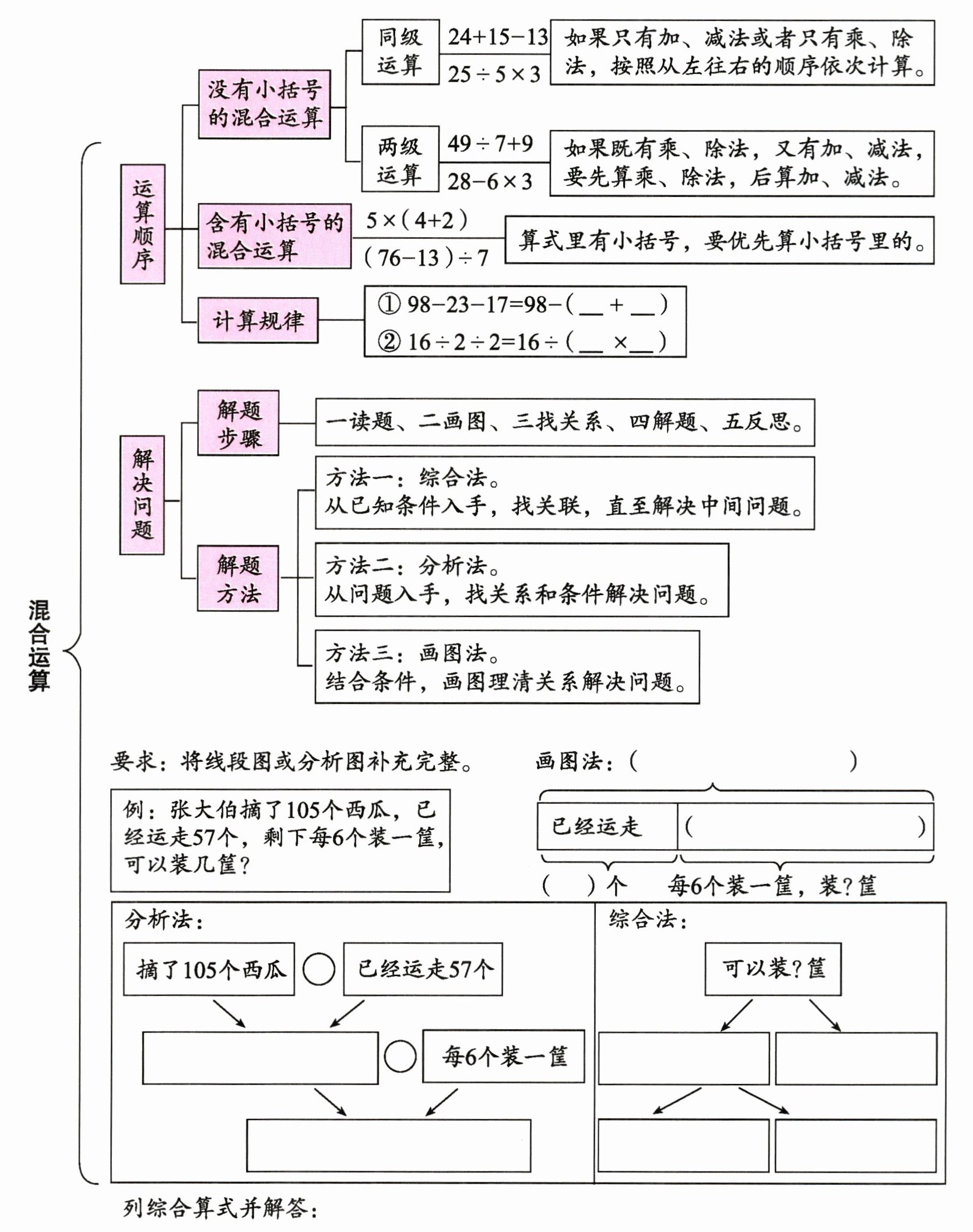
计算规律①：23，17；②：2，2；画图法：剩下的西瓜，105；分析法和综合法：先算105 - 57，再算(105 - 57)÷6；综合算式：(105 - 57)÷6=(48)÷6 = 8（筐），可以装8筐。

答案： 1. 计算规律：
①根据减法的性质$a - b - c=a-(b + c)$，所以$98−23−17 = 98-(23 + 17)$。
②根据除法的性质$a÷ b÷ c=a÷(b× c)$，所以$16÷2÷2 = 16÷(2×2)$。
2. 画图法：
已经运走$57$个，剩下的西瓜数为$105 - 57$，所以括号里填“剩下的西瓜”，总共有$105$个西瓜。
3. 分析法：
先算剩下的西瓜数，用摘的西瓜数$105$个减去运走的$57$个，即$105−57$，再算可以装的筐数，用剩下的西瓜数除以每筐装的$6$个，即$(105 - 57)÷6$。
4. 综合法：
要算可以装的筐数，需要知道剩下的西瓜数和每筐装的个数，剩下的西瓜数$=$摘的西瓜数$-$运走的西瓜数，即$105−57$，然后用剩下的西瓜数除以$6$，即$(105 - 57)÷6$。
5. 列综合算式并解答：
解：
综合算式$(105 - 57)÷6$。
先算括号里：$105−57 = 48$，再算除法：$48÷6=8$（筐）。
综上，计算规律①$23$，$17$；②$2$，$2$；画图法括号依次填“剩下的西瓜”，$105$；分析法和综合法都是先算$105 - 57$，再算$(105 - 57)÷6$；综合算式$(105 - 57)÷6=(48)÷6 = 8$（筐），可以装$8$筐。