《2025年小学生学习指导丛书三年级数学上册人教版》

1. 下图各有 12 个△,分一分,涂一涂,分别找到它的$\frac{1}{6}和\frac{3}{4}$,列式比一比涂色个数是否相同？
$\frac{1}{6}$
$\frac{3}{4}$

答案： 对于$\frac{1}{6}$：
$12×\frac{1}{6} = 2$（个）
涂色个数为2个。
对于$\frac{3}{4}$：
$12×\frac{3}{4}=9$（个）
涂色个数为9个。
2≠9，涂色个数不同。

2. 跳棋 1880 年在英国创立,最初的棋盘是正方形的,共有 256 格。后面逐渐发展成为六角星形。跳棋是一种可以由 2～6 人同时进行的棋,每一位玩家使用跳棋一个角,拥有一种颜色的棋子。它是一种老少咸宜、流传广泛的益智类棋类游戏。

(1) 如图,一颗珠子占

的($\frac{1}{6}$)。
(2)

占整个棋盘珠子的($\frac{1}{6}$)。
(3) 跳棋使用 6 枚棋子叫“六子跳棋”,使用 10 枚棋子叫“十子跳棋”,以此类推。同学们正在玩“十五子跳棋”(每位玩家使用 15 枚跳棋),已知棋盘上黄色珠子占整个棋盘珠子总数的$\frac{1}{6}$,棋盘上一共有多少个珠子？
90

答案：
(1)$\frac{1}{6}$；
(2)$\frac{1}{6}$；
(3)90

3. 算一算。

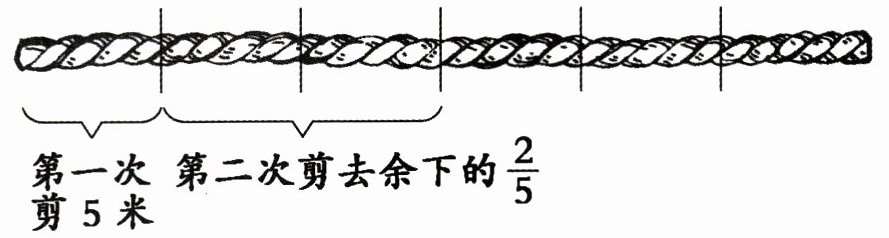
第二次剪去(8)米。

答案： 从图中可知，绳子被平均分成了5大段，总长度看作单位“5”，第一次剪去1大段即$\frac{1}{5}$是5米，所以绳子的总长度为：
$5÷\frac{1}{5}=25$（米）
第一次剪完后余下的长度为：
$25 - 5=20$（米）
第二次剪去余下的$\frac{2}{5}$，则第二次剪去的长度为：
$20×\frac{2}{5}=8$（米）
答案为：8。