《2025年补充习题江苏九年级物理上册苏科版》

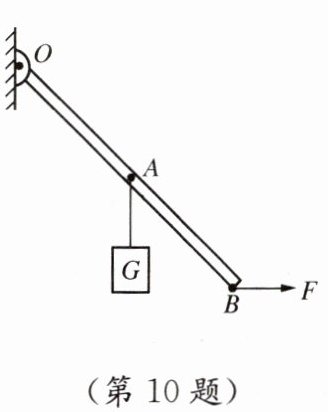
10. 如图所示是一个可绕点O自由转动的轻质杠杆,在杠杆的中点处挂一重物G,在杠杆的另一端施加一个方向始终保持水平向右的力F,使杠杆从图示位置慢慢向水平位置抬起。在此过程中,力F和它的力臂l_F、重力G和它的力臂l_G的变化情况是(A)。

$A.F$增大$,l_F$减小　　
$B.F$减小$,l_F$增大　　
$C.G$不变$,l_G$减小　　
$D.G$变大$,l_G$增大　　

答案： 【解析】：
本题主要考查杠杆平衡条件的应用以及力臂的变化对力的影响。
首先，分析重力$G$和它的力臂$l_G$的变化情况，由于重物$G$始终挂在杠杆的中点处，所以重力$G$的大小是不变的，随着杠杆从图示位置慢慢向水平位置抬起，重物$G$到支点$O$的垂直距离（即力臂$l_G$）实际上是增大的，但在这个特定问题中，我们更关心的是力$F$及其力臂$l_F$的变化。
接着，分析力$F$和它的力臂$l_F$的变化情况，力$F$的方向始终保持水平向右，这意味着力$F$的力臂$l_F$是从支点$O$到力$F$作用点的垂直距离，随着杠杆的抬起，这个垂直距离（即力臂$l_F$）是逐渐减小的，根据杠杆的平衡条件$F_1l_1=F_2l_2$，在重物$G$和它的力臂$l_G$的乘积（即阻力矩）不变的情况下，动力臂$l_F$减小，那么动力$F$必须增大才能保持杠杆的平衡。
【答案】：A.$F$增大，$l_F$减小。

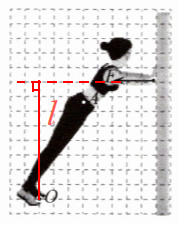
11. 某同学锻炼时,双脚并拢,脚尖O触地,脚后跟踮起,手掌支撑在竖直墙壁上,手臂水平,点A是人体重心所在位置。此时墙壁对手掌的支撑力F如图所示,不计墙壁对手掌的摩擦力,g取10 N/kg。
(1)以O为支点,在图中作出动力F的力臂l。
(2)该同学质量为50 kg,则墙壁对人的支撑力F约为______N。
(3)若增大脚尖与墙壁的距离,手臂仍然水平支撑在墙壁上,支撑力F会______(变大/变小/不变),理由是______。

答案：
$(1) $如图所示　　

$(2) $解：$G=mg=50kg×10N/kg=500N$　　
设动力臂为$l_1，$阻力臂为$l_2，$由杠杆平衡条件$F_1l_1=F_2l_2$得　　
$F×l_1=G×l_2，$观察图像可得，$l_1=8$格，$l_2=3$格　　
$F=G×\frac{l_2}{l_1}=500N×\frac{3}{8}=187.5N$　　
$(3) $变大；增大脚尖与墙壁的距离，动力臂$l_1$变小，阻力$G$不变，阻力臂$l_2$变大，由$F=G\frac{l_2}{l_1}$可知，$F$变大