20. (本小题满分6分)(2024镇江市句容市期中)若$x= m$时,代数式$ax^{2}+bx+c的值也为m$,则称$m$是这个代数式的“x优值”. 例如,当$x= 0$时,代数式$x^{2}-x$的值为0;当$x= 2$时,代数式$x^{2}-x$的值为2,所以0和2都是$x^{2}-x$的“x优值”.
(1) 代数式$x^{2}$的“x优值”是
(2) 判断代数式$x^{2}-x+n^{2}+2$是否存在“x优值”,并说明理由;
(3) 代数式$x^{2}-n^{2}+n$存在两个“x优值”且差为5,求n的值.
(1) 代数式$x^{2}$的“x优值”是
0和1
;(2) 判断代数式$x^{2}-x+n^{2}+2$是否存在“x优值”,并说明理由;
不存在“x优值”.理由如下:假设存在优值为x,则有x² - x + n² + 2=x,整理,得x² - 2x + n² + 2=0,则根的判别式2² - 4(n² + 2)=-4n² - 4.因为无论n取何值时,-4n² - 4 < 0,所以方程没有实数根,即代数式x² - x + n² + 2不存在“x优值”.
(3) 代数式$x^{2}-n^{2}+n$存在两个“x优值”且差为5,求n的值.
设“x优值”为x,则有x² - n² + n=x,整理,得x² - x - n(n - 1)=0,所以(x - n)·(x + n - 1)=0,所以x₁=n,x₂=1 - n.因为两个“x优值”差为5,所以n - (1 - n)=5或(1 - n) - n=5,所以n=3或n=-2.
答案:
解:
(1)0和1
(2)不存在“x优值”.理由如下:假设存在优值为x,则有x² - x + n² + 2=x,整理,得x² - 2x + n² + 2=0,则根的判别式2² - 4(n² + 2)=-4n² - 4.因为无论n取何值时,-4n² - 4 < 0,所以方程没有实数根,即代数式x² - x + n² + 2不存在“x优值”.
(3)设“x优值”为x,则有x² - n² + n=x,整理,得x² - x - n(n - 1)=0,所以(x - n)·(x + n - 1)=0,所以x₁=n,x₂=1 - n.因为两个“x优值”差为5,所以n - (1 - n)=5或(1 - n) - n=5,所以n=3或n=-2.
(1)0和1
(2)不存在“x优值”.理由如下:假设存在优值为x,则有x² - x + n² + 2=x,整理,得x² - 2x + n² + 2=0,则根的判别式2² - 4(n² + 2)=-4n² - 4.因为无论n取何值时,-4n² - 4 < 0,所以方程没有实数根,即代数式x² - x + n² + 2不存在“x优值”.
(3)设“x优值”为x,则有x² - n² + n=x,整理,得x² - x - n(n - 1)=0,所以(x - n)·(x + n - 1)=0,所以x₁=n,x₂=1 - n.因为两个“x优值”差为5,所以n - (1 - n)=5或(1 - n) - n=5,所以n=3或n=-2.
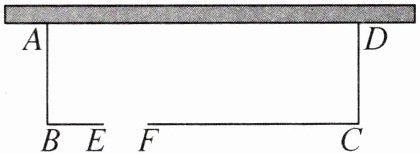
21. (本小题满分6分)如图,老李想用长为70m的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈$ABCD$,并在边$BC$上留一个2m宽的门(建在$EF$处,另用其他材料).
(1) 当羊圈的长和宽分别为多少米时,能围成一个面积为$640m^{2}$的羊圈?
(2) 羊圈的面积能达到$650m^{2}$吗? 如果能,请你给出设计方案;如果不能,请说明理由.
(1) 当羊圈的长和宽分别为多少米时,能围成一个面积为$640m^{2}$的羊圈?
(2) 羊圈的面积能达到$650m^{2}$吗? 如果能,请你给出设计方案;如果不能,请说明理由.

答案:
解:
(1)设AB=x m,则BC的长为70 - 2x + 2=(72 - 2x)m.根据题意,得x(72 - 2x)=640,化简,得x² - 36x + 320=0.解得x₁=16,x₂=20.当x=16时,72 - 2x=72 - 32=40(m);当x=20时,72 - 2x=72 - 40=32(m). 答:当羊圈的长为40 m,宽为16 m或长为32 m,宽为20 m时,能围成一个面积为640 m²的羊圈.
(2)不能.理由如下: 由题意,得x(72 - 2x)=650.化简,得x² - 36x + 325=0.因为根的判别式(-36)² - 4×325=-4 < 0,所以一元二次方程没有实数根,所以羊圈的面积不能达到650 m².
(1)设AB=x m,则BC的长为70 - 2x + 2=(72 - 2x)m.根据题意,得x(72 - 2x)=640,化简,得x² - 36x + 320=0.解得x₁=16,x₂=20.当x=16时,72 - 2x=72 - 32=40(m);当x=20时,72 - 2x=72 - 40=32(m). 答:当羊圈的长为40 m,宽为16 m或长为32 m,宽为20 m时,能围成一个面积为640 m²的羊圈.
(2)不能.理由如下: 由题意,得x(72 - 2x)=650.化简,得x² - 36x + 325=0.因为根的判别式(-36)² - 4×325=-4 < 0,所以一元二次方程没有实数根,所以羊圈的面积不能达到650 m².
22. (本小题满分10分)阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为$x= a$的形式. 求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组. 求解一元二次方程,把它转化为两个一元一次方程来解. 求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验. 各类方程的解法不尽相同,但是它们有一个共同的基本数学思想——转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程. 例如,一元三次方程$x^{3}+x^{2}-2x= 0$,可以通过因式分解把它转化为$x(x^{2}+x-2)= 0$,解方程$x= 0和x^{2}+x-2= 0$,可得方程$x^{3}+x^{2}-2x= 0$的解.
(1) 问题:方程$x^{3}+x^{2}-2x= 0的解是x_{1}= 0$,$x_{2}= $
(2) 拓展:用“转化”思想求方程$\sqrt{2x+3}= x$的解;
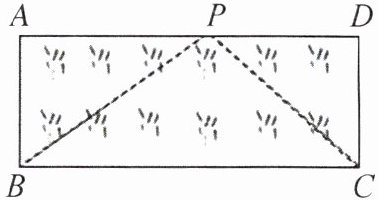
(3) 应用:如图,已知矩形草坪$ABCD的长AD= 8m$,宽$AB= 3m$,小华把一根长为10m的绳子的一端固定在点$B$,沿草坪边$BA$,$AD走到点P$处,把长绳$PB段拉直并固定在点P$,然后沿草坪边$PD$,$DC走到点C$处,把长绳剩下的一段拉直,长绳的另一端恰好落在点$C$. 求$AP$的长.
求解一元一次方程,根据等式的基本性质,把方程转化为$x= a$的形式. 求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组. 求解一元二次方程,把它转化为两个一元一次方程来解. 求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验. 各类方程的解法不尽相同,但是它们有一个共同的基本数学思想——转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程. 例如,一元三次方程$x^{3}+x^{2}-2x= 0$,可以通过因式分解把它转化为$x(x^{2}+x-2)= 0$,解方程$x= 0和x^{2}+x-2= 0$,可得方程$x^{3}+x^{2}-2x= 0$的解.
(1) 问题:方程$x^{3}+x^{2}-2x= 0的解是x_{1}= 0$,$x_{2}= $
-2
,$x_{3}= $1
;(2) 拓展:用“转化”思想求方程$\sqrt{2x+3}= x$的解;
解:方程的两边平方,得2x + 3=x²,整理,得x² - 2x - 3=0,分解因式,得(x - 3)·(x + 1)=0,解得x₁=3,x₂=-1.当x=-1时,$\sqrt{2x + 3}$=1≠-1,所以x=-1不是原方程的解,所以方程$\sqrt{2x + 3}$=x的解是x=3.
(3) 应用:如图,已知矩形草坪$ABCD的长AD= 8m$,宽$AB= 3m$,小华把一根长为10m的绳子的一端固定在点$B$,沿草坪边$BA$,$AD走到点P$处,把长绳$PB段拉直并固定在点P$,然后沿草坪边$PD$,$DC走到点C$处,把长绳剩下的一段拉直,长绳的另一端恰好落在点$C$. 求$AP$的长.

解:因为四边形ABCD是矩形,所以∠A=∠D=90°,CD=AB=3 m.设AP=x m,则PD=(8 - x)m.由勾股定理,得BP=$\sqrt{AP^{2}+AB^{2}}$,CP=$\sqrt{CD^{2}+PD^{2}}$.因为BP + CP=10 m,所以$\sqrt{9 + x^{2}}$ + $\sqrt{(8 - x)^{2}+9}$=10,所以$\sqrt{(8 - x)^{2}+9}$=10 - $\sqrt{9 + x^{2}}$,两边平方,得(8 - x)² + 9=100 - 20$\sqrt{9 + x^{2}}$ + 9 + x²,整理,得5$\sqrt{x^{2}+9}$=4x + 9,两边平方并整理,得x² - 8x + 16=0,即(x - 4)²=0,解得x=4.经检验,x=4是方程的解. 答:AP的长为4 m.
答案:
解:
(1)-2 1
(2)方程的两边平方,得2x + 3=x²,整理,得x² - 2x - 3=0,分解因式,得(x - 3)·(x + 1)=0,解得x₁=3,x₂=-1.当x=-1时,$\sqrt{2x + 3}$=1≠-1,所以x=-1不是原方程的解,所以方程$\sqrt{2x + 3}$=x的解是x=3.
(3)因为四边形ABCD是矩形,所以∠A=∠D=90°,CD=AB=3 m.设AP=x m,则PD=(8 - x)m.由勾股定理,得BP=$\sqrt{AP^{2}+AB^{2}}$,CP=$\sqrt{CD^{2}+PD^{2}}$.因为BP + CP=10 m,所以$\sqrt{9 + x^{2}}$ + $\sqrt{(8 - x)^{2}+9}$=10,所以$\sqrt{(8 - x)^{2}+9}$=10 - $\sqrt{9 + x^{2}}$,两边平方,得(8 - x)² + 9=100 - 20$\sqrt{9 + x^{2}}$ + 9 + x²,整理,得5$\sqrt{x^{2}+9}$=4x + 9,两边平方并整理,得x² - 8x + 16=0,即(x - 4)²=0,解得x=4.经检验,x=4是方程的解. 答:AP的长为4 m.
(1)-2 1
(2)方程的两边平方,得2x + 3=x²,整理,得x² - 2x - 3=0,分解因式,得(x - 3)·(x + 1)=0,解得x₁=3,x₂=-1.当x=-1时,$\sqrt{2x + 3}$=1≠-1,所以x=-1不是原方程的解,所以方程$\sqrt{2x + 3}$=x的解是x=3.
(3)因为四边形ABCD是矩形,所以∠A=∠D=90°,CD=AB=3 m.设AP=x m,则PD=(8 - x)m.由勾股定理,得BP=$\sqrt{AP^{2}+AB^{2}}$,CP=$\sqrt{CD^{2}+PD^{2}}$.因为BP + CP=10 m,所以$\sqrt{9 + x^{2}}$ + $\sqrt{(8 - x)^{2}+9}$=10,所以$\sqrt{(8 - x)^{2}+9}$=10 - $\sqrt{9 + x^{2}}$,两边平方,得(8 - x)² + 9=100 - 20$\sqrt{9 + x^{2}}$ + 9 + x²,整理,得5$\sqrt{x^{2}+9}$=4x + 9,两边平方并整理,得x² - 8x + 16=0,即(x - 4)²=0,解得x=4.经检验,x=4是方程的解. 答:AP的长为4 m.
查看更多完整答案,请扫码查看


