第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
13. (2024·文山州文山市期末)黄亮同学看到滑雪运动员从越陡的坡滑下时,越快滑到底端。对此他猜想:“斜面坡度不同,物体从静止开始滑到底端的平均速度也不同”。请你设计实验验证其猜想。
实验所需的公式:$v=\frac{s}{t}$
实验器材:长木板、木块、滑块、秒表、刻度尺。
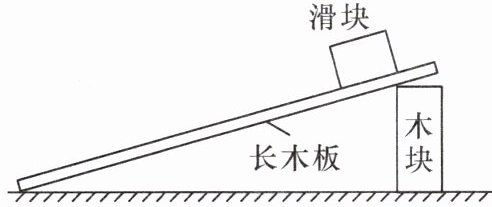
实验步骤:
(1)如图,用刻度尺测出滑块滑动的距离为 s,测出通过该距离所用时间为$t_{1}$。
(2)
(3)若$t_{1}≠t_{2}$,说明
实验所需的公式:$v=\frac{s}{t}$
实验器材:长木板、木块、滑块、秒表、刻度尺。

实验步骤:
(1)如图,用刻度尺测出滑块滑动的距离为 s,测出通过该距离所用时间为$t_{1}$。
(2)
用木块改变斜面坡度,滑块从同一位置静止释放
,用秒表再测出滑块滑动相同距离 s 的时间$t_{2}$。(3)若$t_{1}≠t_{2}$,说明
斜面坡度不同,平均速度不同
。
答案:
13.
(2)用木块改变斜面坡度,滑块从同一位置静止释放
(3)斜面坡度不同,平均速度不同
(2)用木块改变斜面坡度,滑块从同一位置静止释放
(3)斜面坡度不同,平均速度不同
14. (2024·云大附中期末)阅读下列材料,回答问题。
意大利科学家伽利略是物理学的伟大先驱。他在比萨大教堂参加活动时,教堂穹顶上的吊灯因风吹过不停地摆动。他发现,尽管吊灯的摆动幅度越来越小,但每一次摆动的时间似乎相等。
伽利略知道脉搏的跳动是有规律的,于是便按着脉注视着灯的摆动,发现每往返摆动一次的时间的确相同。这使他又冒出一个疑问:假如吊灯受到强风吹动,摆得高了一些,以后每次摆动的时间还是一样的吗?回到宿舍后,他用铁块制成一个摆,把铁块拉到不同高度,用脉搏细心地测定摆动所用的时间。结果表明,每次摆动的时间仍然相同,即“不论摆动的幅度大些还是小些,完成一次摆动的时间是一样的”。这在物理学中叫作“摆的等时性”。各种机械摆钟都是根据这个原理制作的。后来,他又把不同质量的铁块系在绳端作摆锤进行实验。发现,只要用同一条摆绳,摆动一次的时间不受摆锤质量的影响。随后伽利略又想,如果将绳缩短,会不会摆动得快些?于是他用相同的摆锤,用不同的绳长做实验,实验结果证明:“摆绳越长,往复摆动一次的时间(称为周期)就越长。”
伽利略逝世 30 多年后,荷兰物理学家惠更斯找到 了摆的周期与摆长间的数学关系。摆的等时性研究,使人们对钟表的计时研究得到了发展,方便了人们的生活。

请根据上述材料回答下列问题:
(1)摆的摆动快慢与摆球的质量
(2)摆绳越长,摆的摆动就越
(3)实际生活中的摆,可抽象成一根不可伸长的细线和一个体积可忽略的小球组成的单摆模型。如图甲所示,A、B 两点等高,O 点在悬挂点 P 的正下方,若不计空气阻力,小球从 A 点静止释放经 O 点到达 B 点,依据对称性从 A 点到 O 点的时间和从 O 点到 B 点的时间相等。
①如图乙所示,若小球从 A 点静止释放经过 O 点到 B 点的时间为 t,从 A’点静止释放经过 O 点到 B’点的时间为 t’,A、B 两点等高,A’、B’两点等高,则 t’
②若小球从 A 点静止释放后,摆到最低点时由于摆线碰到固定在 P 点正下方 P’处的障碍物,使得小球只能绕 P’点上摆到与 A 点等高的 C 点,如图丙所示,则小球从 A 点到 O 点的时间$t_{AO}$和小球从 O 点到 C 点的时间$t_{OC}$的大小关系为:$t_{AO}$
意大利科学家伽利略是物理学的伟大先驱。他在比萨大教堂参加活动时,教堂穹顶上的吊灯因风吹过不停地摆动。他发现,尽管吊灯的摆动幅度越来越小,但每一次摆动的时间似乎相等。
伽利略知道脉搏的跳动是有规律的,于是便按着脉注视着灯的摆动,发现每往返摆动一次的时间的确相同。这使他又冒出一个疑问:假如吊灯受到强风吹动,摆得高了一些,以后每次摆动的时间还是一样的吗?回到宿舍后,他用铁块制成一个摆,把铁块拉到不同高度,用脉搏细心地测定摆动所用的时间。结果表明,每次摆动的时间仍然相同,即“不论摆动的幅度大些还是小些,完成一次摆动的时间是一样的”。这在物理学中叫作“摆的等时性”。各种机械摆钟都是根据这个原理制作的。后来,他又把不同质量的铁块系在绳端作摆锤进行实验。发现,只要用同一条摆绳,摆动一次的时间不受摆锤质量的影响。随后伽利略又想,如果将绳缩短,会不会摆动得快些?于是他用相同的摆锤,用不同的绳长做实验,实验结果证明:“摆绳越长,往复摆动一次的时间(称为周期)就越长。”
伽利略逝世 30 多年后,荷兰物理学家惠更斯找到 了摆的周期与摆长间的数学关系。摆的等时性研究,使人们对钟表的计时研究得到了发展,方便了人们的生活。

请根据上述材料回答下列问题:
(1)摆的摆动快慢与摆球的质量
无关
(填“无关”或“有关”)。(2)摆绳越长,摆的摆动就越
慢
(填“快”或“慢”)。(3)实际生活中的摆,可抽象成一根不可伸长的细线和一个体积可忽略的小球组成的单摆模型。如图甲所示,A、B 两点等高,O 点在悬挂点 P 的正下方,若不计空气阻力,小球从 A 点静止释放经 O 点到达 B 点,依据对称性从 A 点到 O 点的时间和从 O 点到 B 点的时间相等。
①如图乙所示,若小球从 A 点静止释放经过 O 点到 B 点的时间为 t,从 A’点静止释放经过 O 点到 B’点的时间为 t’,A、B 两点等高,A’、B’两点等高,则 t’
=
t。(填“=”“>”或“<”)②若小球从 A 点静止释放后,摆到最低点时由于摆线碰到固定在 P 点正下方 P’处的障碍物,使得小球只能绕 P’点上摆到与 A 点等高的 C 点,如图丙所示,则小球从 A 点到 O 点的时间$t_{AO}$和小球从 O 点到 C 点的时间$t_{OC}$的大小关系为:$t_{AO}$
>
$t_{OC}$。(填“=”“>”或“<”)
答案:
14.
(1)无关
(2)慢
(3)①= ②>
(1)无关
(2)慢
(3)①= ②>
查看更多完整答案,请扫码查看


