2025年暑假作业贵州人民出版社四年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业贵州人民出版社四年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 一个等腰三角形的一个底角与顶角的度数和是$125^{\circ }$,它的一个底角是多少度?顶角是多少度?
答案:
底角:$ 180^{\circ} - 125^{\circ} = 55^{\circ} $
顶角:$ 125^{\circ} - 55^{\circ} = 70^{\circ} $
顶角:$ 125^{\circ} - 55^{\circ} = 70^{\circ} $
3. 下面是两块三角形的玻璃打碎后留下的碎片,你知道它们原来各是什么三角形吗?
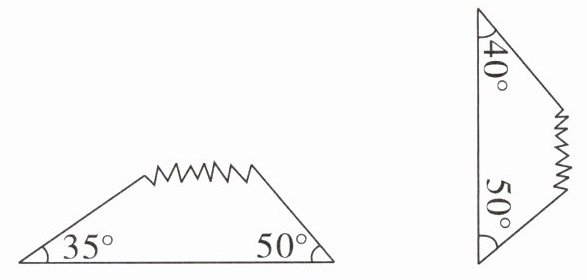

答案:
$ 180^{\circ} - 35^{\circ} - 50^{\circ} = 95^{\circ} $,钝角三角形
$ 180^{\circ} - 40^{\circ} - 50^{\circ} = 90^{\circ} $,直角三角形
$ 180^{\circ} - 40^{\circ} - 50^{\circ} = 90^{\circ} $,直角三角形
4. 如图,将三角形 ABC 的三个角分别沿 DE,HG,EF 翻折,三个顶点均落在点 O 处。
(1)根据三角形 ABC 的内角和求出$∠1+∠2$的度数。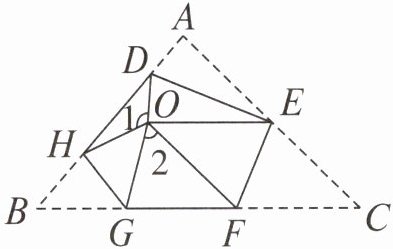
(2)求出翻折后得到的五边形 HGFED 的内角和。
(1)根据三角形 ABC 的内角和求出$∠1+∠2$的度数。

(2)求出翻折后得到的五边形 HGFED 的内角和。
答案:
(1) $ \angle 1 $、$ \angle 2 $ 与三角形 $ ABC $ 翻折起来的三个角组成了一个周角,所以 $ \angle 1 + \angle 2 = 360^{\circ} - 180^{\circ} = 180^{\circ} $。
(2) $ 180^{\circ} × (5 - 2) = 540^{\circ} $
(1) $ \angle 1 $、$ \angle 2 $ 与三角形 $ ABC $ 翻折起来的三个角组成了一个周角,所以 $ \angle 1 + \angle 2 = 360^{\circ} - 180^{\circ} = 180^{\circ} $。
(2) $ 180^{\circ} × (5 - 2) = 540^{\circ} $
5. 一个零件如图所示,$∠1= 32^{\circ },∠2= 25^{\circ }$,当$∠3= 90^{\circ }$时才符合要求,工人师傅在检验时,只量了$∠4= 145^{\circ }$,他说:“这个零件不符 合要求。”你知道这是为什么吗?
合要求。”你知道这是为什么吗?
 合要求。”你知道这是为什么吗?
合要求。”你知道这是为什么吗?
答案:
添加辅助线如图所示。

$ \angle 1 + \angle 3 + \angle 6 = 180^{\circ} $,$ \angle 5 + \angle 6 = 180^{\circ} $,$ \angle 1 + \angle 3 = \angle 5 $;同理,$ \angle 4 = \angle 5 + \angle 2 = \angle 1 + \angle 3 + \angle 2 = 32^{\circ} + 90^{\circ} + 25^{\circ} = 147^{\circ} $,$ 147^{\circ} > 145^{\circ} $,所以这个零件不符合要求。
添加辅助线如图所示。

$ \angle 1 + \angle 3 + \angle 6 = 180^{\circ} $,$ \angle 5 + \angle 6 = 180^{\circ} $,$ \angle 1 + \angle 3 = \angle 5 $;同理,$ \angle 4 = \angle 5 + \angle 2 = \angle 1 + \angle 3 + \angle 2 = 32^{\circ} + 90^{\circ} + 25^{\circ} = 147^{\circ} $,$ 147^{\circ} > 145^{\circ} $,所以这个零件不符合要求。
查看更多完整答案,请扫码查看


