《2025年卓远暑假生活河北美术出版社八年级数学》

2. 如图6,矩形$ABCD$为一个花园,其中$AB = 15 \mathrm { m }$,$BC = 8 \mathrm { m }$,在花园内修一条长$13 \mathrm { m }的笔直小路EF$,小路出口一端$E选在AD边上距点D 3 \mathrm { m }$处,另一端出口$F应选在AB边上距点B$3米处？

答案： 解：由题意知$EF=13m$，$EA=5m$。
在$Rt\triangle EAF$中，由勾股定理，得
$AF^{2}=EF^{2}-EA^{2}$，
即$AF^{2}=13^{2}-5^{2}=144$，
则$AF=12m$（取正值）。
所以$FB=15-12=3(m)$，
即$F$应选在$AB$边上距点$B3m$处。

3. 如图7,$E$,$F分别是正方形ABCD的边CB$,$DC$延长线上的点,且$BE = CF$,过点$E作EG // BF$,交正方形外角的平分线$CG于点G$,连接$GF$.
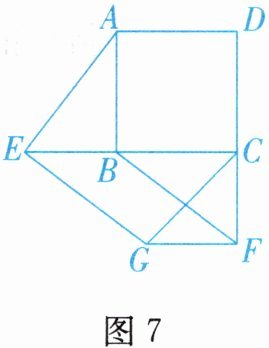
求证：(1)$AE \perp BF$；(2)四边形$BEGF$是平行四边形.

答案：
证明：
(1)$\because$四边形$ABCD$是正方形，
$\therefore AB=BC$，$\angle ABC=\angle BCD=90^{\circ}$，
$\therefore \angle ABE=\angle BCF=90^{\circ}$，
又知$BE=CF$，
$\therefore \triangle ABE\cong\triangle BCF(SAS)$，
$\therefore AE=BF$，$\angle BAE=\angle CBF$，
$\because EG// BF$，$\therefore \angle CBF=\angle CEG$，
$\because \angle BAE+\angle BEA=90^{\circ}$，
$\therefore \angle CEG+\angle BEA=90^{\circ}$，
$\therefore AE\perp EG$，$\therefore AE\perp BF$。
(2)延长$AB$至点$P$，使$BP=BE$，连接$EP$，如图所示:
则$AP=CE$，
$\angle EBP=90^{\circ}$，
$\therefore \angle P=45^{\circ}$，

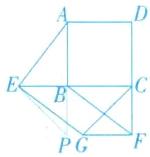
$\because CG$为$\angle BCF$的平分线，
$\therefore \angle ECG=45^{\circ}$，
$\therefore \angle P=\angle ECG$，
由
(1)得$\angle BAE=\angle CEG$，
$\therefore \triangle APE\cong\triangle ECG(ASA)$，
$\therefore AE=EG$，
$\because AE=BF$，$\therefore EG=BF$，
$\because EG// BF$，
$\therefore$四边形$BEGF$是平行四边形。