《2025年快乐暑假四年级四川大学出版社》

四、用你的巧手拼一拼,在能拼成三角形的各组小棒下面画“√”。(单位:厘米)

√ √ √ ×

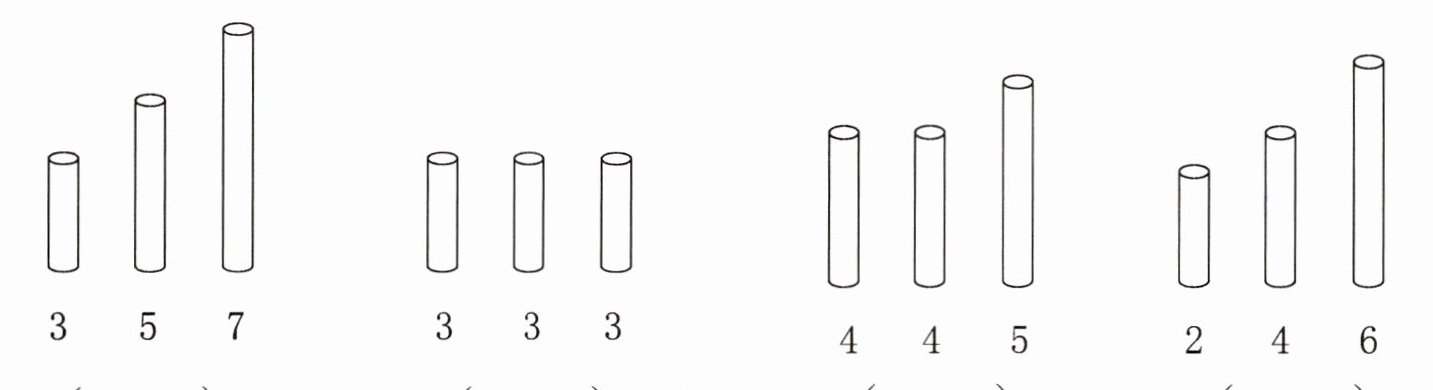
答案： √ √ √ ×

五、在下面的网格中画三角形:
1. 一个等边三角形;

2. 既是直角三角形又是等腰三角形;
3. 既是锐角三角形又是等腰三角形。

答案： 【解析】：
1. 对于等边三角形，需要三条边长度相等。在网格中，可以通过选择格点使得三条边长度相等来构造。
2. 对于既是直角三角形又是等腰三角形的情况，需要找到一个直角，并且两条直角边长度相等。
3. 对于既是锐角三角形又是等腰三角形的情况，需要确保所有角都是锐角，并且至少有两边长度相等。
【答案】：
1. 一个等边三角形（答案不唯一）：
在网格上选择三个点，例如(0,0)，(2,0)，(1,$\sqrt{3}$)（假设网格边长为1，利用等边三角形的高与边长的关系确定第三个点），连接这三个点形成一个等边三角形。由于网格限制，可以通过近似的方式在网格上找到接近等边三角形的形状。
图略。
2. 既是直角三角形又是等腰三角形（答案不唯一）：
在网格上选择点，如(0,0)，(0,2)，(2,0)，连接这三个点形成一个直角三角形，其中两条直角边长度相等（都是2个单位长度），满足等腰直角三角形的条件。
图略。
3. 既是锐角三角形又是等腰三角形（答案不唯一）：
在网格上选择点，如(1,1)，(3,1)，(2,2)，连接这三个点形成一个三角形。这个三角形的三个角都是锐角，并且有两边长度相等（从(1,1)到(3,1)和从(1,1)到(2,2)的距离相等，都是$\sqrt{5}$个单位长度，利用勾股定理计算得出），满足锐角等腰三角形的条件。
图略。

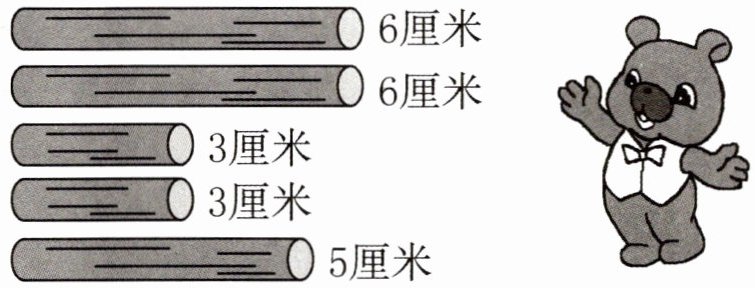
1. 小熊要建一座漂亮的房子,请你帮它选择三根木料作为房子的三脚架(如图),并说明你的选择理由。

答案： 【解析】：
本题可根据三角形三边关系“任意两边之和大于第三边，任意两边之差小于第三边”来选择合适的三根木料作为房子的三脚架。
需要从给定的木料长度$6$厘米、$6$厘米、$3$厘米、$3$厘米、$5$厘米中选取三根，然后判断能否构成三角形。
分别列举不同的组合情况进行分析：
组合一：$3$厘米、$3$厘米、$5$厘米。
计算$3 + 3 = 6$（厘米），$6\gt 5$；$5 - 3 = 2$（厘米），$2\lt 3$，满足三角形三边关系。
组合二：$3$厘米、$3$厘米、$6$厘米。
计算$3 + 3 = 6$（厘米），不满足“任意两边之和大于第三边”，所以不能构成三角形。
组合三：$3$厘米、$5$厘米、$6$厘米。
计算$3 + 5 = 8$（厘米），$8\gt 6$；$6 - 3 = 3$（厘米），$3\lt 5$；$6 - 5 = 1$（厘米），$1\lt 3$，满足三角形三边关系。
组合四：$5$厘米、$6$厘米、$6$厘米。
计算$5 + 6 = 11$（厘米），$11\gt 6$；$6 - 5 = 1$（厘米），$1\lt 6$；$6 - 6 = 0$（厘米），$0\lt 5$，满足三角形三边关系。
【答案】：
选择$3$厘米、$3$厘米、$5$厘米或$3$厘米、$5$厘米、$6$厘米或$5$厘米、$6$厘米、$6$厘米这三组木料中的任意一组。
理由：根据三角形三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，这三组木料都满足该关系，所以可以构成三角形作为房子的三脚架。