【题目】二次函数 ![]() 的图象与
的图象与 ![]() 轴交于
轴交于 ![]() (1, 0),
(1, 0), ![]() 两点,与
两点,与 ![]() 轴交于点
轴交于点 ![]() ,其顶点
,其顶点 ![]() 的坐标为(-3, 2).
的坐标为(-3, 2).
(1)求这二次函数的关系式;
(2)求 ![]() 的面积.
的面积.
参考答案:
【答案】
(1)解:∵二次函数y=ax2+bx+c的图象的顶点D的坐标为(-3,2),
∴设抛物线解析式为顶点式y=a(x+3)2+2(a≠0),
把点A(1,0)代入,得
a(1+3)2+2=0,
解得,a=- ![]() ,
,
则抛物线的解析式为:y=- ![]() (x+3)2+2
(x+3)2+2
(2)解:∵二次函数y=- ![]() (x+3)2+2的图象与x轴交于A(1,0)、B两点,顶点D的坐标为(-3,2),
(x+3)2+2的图象与x轴交于A(1,0)、B两点,顶点D的坐标为(-3,2),
∴点B的横坐标是2×(-3)-1=-7,则B(-7,0).
令x=0,则y= ![]() ,
,
∴C(0, ![]() ).
).
易求直线BC的解析式为:y= ![]() x+
x+ ![]() .
.
∴当x=-3时,y= ![]() ,
,
∴PD=2- ![]() =1.5,
=1.5,
∴△PBC的面积= ![]() PDOB=
PDOB= ![]() ×1.5×7=5.25
×1.5×7=5.25
【解析】(1)由二次函数y=ax2+bx+c的图象的顶点D的坐标为(-3,2),得到顶点式,把A点的坐标代入顶点式,求出a的值,得到抛物线的解析式;(2)由二次函数的图象与x轴交于A、B两点和顶点D的坐标,求出点B的坐标,得到点C的坐标,求出直线BC的解析式,求出ΔBCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙
是⊙  的直径,
的直径,  、
、  为⊙
为⊙  上位于
上位于  异侧的两点,连接
异侧的两点,连接  并延长至点
并延长至点  ,使得
,使得  ,连接
,连接  交⊙
交⊙  于点
于点 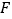 ,连接
,连接 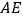 、
、  、
、  .
.
(1)证明: ;
;
(2)若 ,求
,求  的度数;
的度数;
(3)设 交
交  于点
于点  ,若
,若  是
是  的中点,求
的中点,求  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线
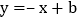 与x轴正半轴,y轴正半轴分别交于点A,B,点
与x轴正半轴,y轴正半轴分别交于点A,B,点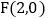 ,点E在第一象限,
,点E在第一象限,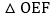 为等边三角形,连接AE,BE
为等边三角形,连接AE,BE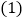 求点E的坐标;
求点E的坐标;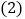 当BE所在的直线将
当BE所在的直线将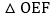 的面积分为3:1时,求
的面积分为3:1时,求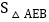 的面积;
的面积;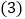 取线段AB的中点P,连接PE,OP,当
取线段AB的中点P,连接PE,OP,当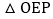 是以OE为腰的等腰三角形时,则
是以OE为腰的等腰三角形时,则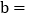 ______
______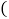 直接写出b的值
直接写出b的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次向右跳动至A1(-1,1),第二次向左跳动至A2(2,1),第三次向右跳动至A3(-2,2),第四次向左跳动至A4(3,2)依照此规律跳动下去,点A第2020次跳动至A2020的坐标为__________.

-
科目: 来源: 题型:
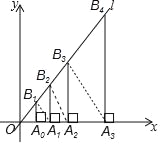
查看答案和解析>>【题目】如图,过点A0(1,0)作x轴的垂线,交直线l:y=2x于B1,在x轴上取点A1,使OA1=OB1,过点A1作x轴的垂线,交直线l于B2,在x轴上取点A2,使OA2=OB2,过点A2作x轴的垂线,交直线l于B3,…,这样依次作图,则点B8的纵坐标为( )
A. (
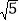 )7B. 2(
)7B. 2(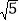 )7C. 2(
)7C. 2(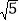 )8D. (
)8D. (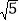 )9
)9 -
科目: 来源: 题型:
查看答案和解析>>【题目】某农场去年种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为
 .
.
(1)则今年南瓜的种植面积为亩;(用含 的代数式表示)
的代数式表示)
(2)如果今年南瓜亩产量的增长率是种植面积的增长率的 ,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率. -
科目: 来源: 题型:
查看答案和解析>>【题目】小莉手中有块周长为100cm的长方形硬纸片,其中长比宽多10cm.
(1)求长方形的面积;
(2)小莉想用这块长方形的硬纸片,沿着边的方向裁出一块长与宽的比为5:4,面积为720cm2的新纸片另作他用,请判断小莉能否成功,并说明理由.
相关试题

