【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次向右跳动至A1(-1,1),第二次向左跳动至A2(2,1),第三次向右跳动至A3(-2,2),第四次向左跳动至A4(3,2)依照此规律跳动下去,点A第2020次跳动至A2020的坐标为__________.

参考答案:
【答案】![]()
【解析】
根据图形观察发现,第偶数次跳动至点的坐标,横坐标是次数的一半加上1,纵坐标是次数的一半,奇数次跳动与该偶数次跳动的横坐标的相反数加上1,纵坐标相同,然后写出即可.
解:如图

观察发现,第2次跳动至点的坐标是![]() ,
,
第4次跳动至点的坐标是![]() ,
,
第6次跳动至点的坐标是![]() ,
,
第8次跳动至点的坐标是![]() ,
,
![]()
第![]() 次跳动至点的坐标是
次跳动至点的坐标是![]() ,
,
则第2020次跳动至点的坐标是![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“足球进校园”的号召,学校开设了足球兴趣拓展班,计划同时购买A,B两种足球30个,A,B两种足球的价格分别为50元
 个,80元
个,80元 个,设购买B种足球x个,购买两种足球的总费用为y元.
个,设购买B种足球x个,购买两种足球的总费用为y元. 求y关于x的函数表达式.
求y关于x的函数表达式. 在总费用不超过1600元的前提下,从节省费用的角度来考虑,求总费用的最小值.
在总费用不超过1600元的前提下,从节省费用的角度来考虑,求总费用的最小值. 因足球兴趣拓展班的人数增多,所以实际购买中这两种足球总数超过30个,总费用为2000元,则该学校可能共购买足球______个
因足球兴趣拓展班的人数增多,所以实际购买中这两种足球总数超过30个,总费用为2000元,则该学校可能共购买足球______个 直接写出答案
直接写出答案
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙
是⊙  的直径,
的直径,  、
、  为⊙
为⊙  上位于
上位于  异侧的两点,连接
异侧的两点,连接  并延长至点
并延长至点  ,使得
,使得  ,连接
,连接  交⊙
交⊙  于点
于点 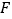 ,连接
,连接 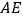 、
、  、
、  .
.
(1)证明: ;
;
(2)若 ,求
,求  的度数;
的度数;
(3)设 交
交  于点
于点  ,若
,若  是
是  的中点,求
的中点,求  的值.
的值. -
科目: 来源: 题型:
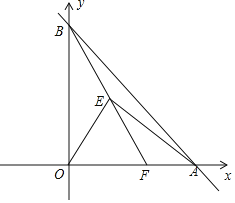
查看答案和解析>>【题目】如图,在直角坐标系中,直线
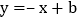 与x轴正半轴,y轴正半轴分别交于点A,B,点
与x轴正半轴,y轴正半轴分别交于点A,B,点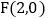 ,点E在第一象限,
,点E在第一象限, 为等边三角形,连接AE,BE
为等边三角形,连接AE,BE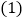 求点E的坐标;
求点E的坐标; 当BE所在的直线将
当BE所在的直线将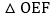 的面积分为3:1时,求
的面积分为3:1时,求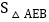 的面积;
的面积;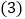 取线段AB的中点P,连接PE,OP,当
取线段AB的中点P,连接PE,OP,当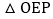 是以OE为腰的等腰三角形时,则
是以OE为腰的等腰三角形时,则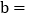 ______
______ 直接写出b的值
直接写出b的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 的图象与
的图象与  轴交于
轴交于  (1, 0),
(1, 0), 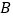 两点,与
两点,与  轴交于点
轴交于点  ,其顶点
,其顶点  的坐标为(-3, 2).
的坐标为(-3, 2).
(1)求这二次函数的关系式;
(2)求 的面积.
的面积. -
科目: 来源: 题型:
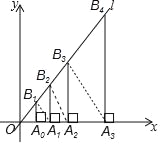
查看答案和解析>>【题目】如图,过点A0(1,0)作x轴的垂线,交直线l:y=2x于B1,在x轴上取点A1,使OA1=OB1,过点A1作x轴的垂线,交直线l于B2,在x轴上取点A2,使OA2=OB2,过点A2作x轴的垂线,交直线l于B3,…,这样依次作图,则点B8的纵坐标为( )
A. (
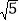 )7B. 2(
)7B. 2(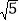 )7C. 2(
)7C. 2(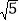 )8D. (
)8D. (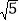 )9
)9 -
科目: 来源: 题型:
查看答案和解析>>【题目】某农场去年种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为
 .
.
(1)则今年南瓜的种植面积为亩;(用含 的代数式表示)
的代数式表示)
(2)如果今年南瓜亩产量的增长率是种植面积的增长率的 ,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
相关试题

