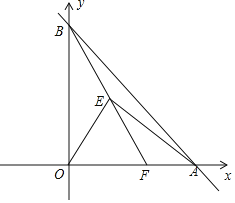
【题目】如图,在直角坐标系中,直线![]() 与x轴正半轴,y轴正半轴分别交于点A,B,点
与x轴正半轴,y轴正半轴分别交于点A,B,点![]() ,点E在第一象限,
,点E在第一象限,![]() 为等边三角形,连接AE,BE
为等边三角形,连接AE,BE
![]() 求点E的坐标;
求点E的坐标;
![]() 当BE所在的直线将
当BE所在的直线将![]() 的面积分为3:1时,求
的面积分为3:1时,求![]() 的面积;
的面积;
![]() 取线段AB的中点P,连接PE,OP,当
取线段AB的中点P,连接PE,OP,当![]() 是以OE为腰的等腰三角形时,则
是以OE为腰的等腰三角形时,则![]() ______
______![]() 直接写出b的值
直接写出b的值![]()
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
![]() 根据等边三角形的性质可得高线EC的长,可得E的坐标;
根据等边三角形的性质可得高线EC的长,可得E的坐标;
![]() 如图2,当BE所在的直线将
如图2,当BE所在的直线将![]() 的面积分为3:1时,存在两种情况:
的面积分为3:1时,存在两种情况:![]() 如图2,
如图2,![]() :
:![]() :1,即OD:
:1,即OD:![]() :1,
:1,![]() :
:![]() :3,即OD:
:3,即OD:![]() :3,先确认DE的解析式,可得OA和OB的长,根据面积差可得结论;
:3,先确认DE的解析式,可得OA和OB的长,根据面积差可得结论;
![]() 存在两种情况:
存在两种情况:![]() 如图3,
如图3,![]() ,作辅助线,构建矩形和高线ED和EM,根据三角形AOB面积的两种求法列等式可得b的值,
,作辅助线,构建矩形和高线ED和EM,根据三角形AOB面积的两种求法列等式可得b的值,![]() 如图4,
如图4,![]() ,根据等腰三角形和等边三角形的性质可得b的值.
,根据等腰三角形和等边三角形的性质可得b的值.
解:![]() 如图1,过E作
如图1,过E作![]() 轴于C,
轴于C,
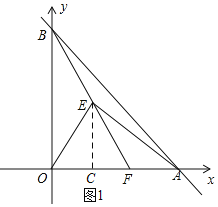
![]() 点
点![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 当BE所在的直线将
当BE所在的直线将![]() 的面积分为3:1时,存在两种情况:
的面积分为3:1时,存在两种情况:
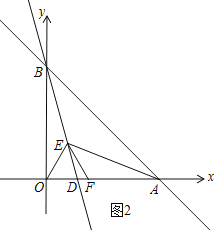
![]() 如图2,
如图2,![]() :
:![]() :1,即OD:
:1,即OD:![]() :1,
:1,
![]() ,
,
![]() ,
,
![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
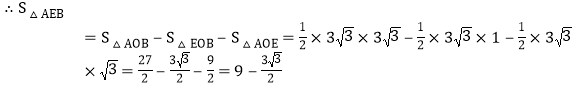 ;
;
![]() :
:![]() :3,即OD:
:3,即OD:![]() :3,
:3,
![]() ,
,
![]() ,
,
![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,
![]() 点B在y轴正半轴上,
点B在y轴正半轴上,
![]() 此种情况不符合题意;
此种情况不符合题意;
综上,![]() 的面积是
的面积是![]() ;
;
![]() 存在两种情况:
存在两种情况:
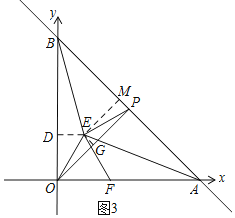
![]() 如图3,
如图3,![]() ,过E作
,过E作![]() 轴于D,作
轴于D,作![]() 于M,作
于M,作![]() 于G,
于G,
![]() 是等腰直角三角形,P是AB的中点,
是等腰直角三角形,P是AB的中点,
![]() ,
,
![]() ,
,
![]() 四边形EGPM是矩形,
四边形EGPM是矩形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
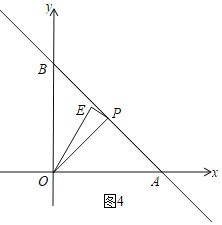
![]() 如图4,当
如图4,当![]() 时,则
时,则![]() ,
,
![]() 是等腰直角三角形,P是AB的中点,
是等腰直角三角形,P是AB的中点,
![]() ,
,
![]() ,即
,即![]() ,
,
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2-6ax+4a+3的图像与y轴交于点A,点B是x轴上一点,其坐标为(1,0),连接AB,tan∠ABO=2.

(1)则点A的坐标为 , a=;
(2)过点A作AB的垂线与该二次函数的图像交于另一点C,求点C的坐标;
(3)连接BC,过点A作直线l交线段BC于点P,设点B、点C到l的距离分别为d1、d2 , 求d1+d2的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“足球进校园”的号召,学校开设了足球兴趣拓展班,计划同时购买A,B两种足球30个,A,B两种足球的价格分别为50元
 个,80元
个,80元 个,设购买B种足球x个,购买两种足球的总费用为y元.
个,设购买B种足球x个,购买两种足球的总费用为y元. 求y关于x的函数表达式.
求y关于x的函数表达式. 在总费用不超过1600元的前提下,从节省费用的角度来考虑,求总费用的最小值.
在总费用不超过1600元的前提下,从节省费用的角度来考虑,求总费用的最小值. 因足球兴趣拓展班的人数增多,所以实际购买中这两种足球总数超过30个,总费用为2000元,则该学校可能共购买足球______个
因足球兴趣拓展班的人数增多,所以实际购买中这两种足球总数超过30个,总费用为2000元,则该学校可能共购买足球______个 直接写出答案
直接写出答案
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙
是⊙  的直径,
的直径,  、
、  为⊙
为⊙  上位于
上位于  异侧的两点,连接
异侧的两点,连接  并延长至点
并延长至点  ,使得
,使得  ,连接
,连接  交⊙
交⊙  于点
于点  ,连接
,连接  、
、  、
、  .
.
(1)证明: ;
;
(2)若 ,求
,求  的度数;
的度数;
(3)设 交
交  于点
于点  ,若
,若  是
是  的中点,求
的中点,求  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次向右跳动至A1(-1,1),第二次向左跳动至A2(2,1),第三次向右跳动至A3(-2,2),第四次向左跳动至A4(3,2)依照此规律跳动下去,点A第2020次跳动至A2020的坐标为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 的图象与
的图象与  轴交于
轴交于  (1, 0),
(1, 0),  两点,与
两点,与  轴交于点
轴交于点  ,其顶点
,其顶点  的坐标为(-3, 2).
的坐标为(-3, 2).
(1)求这二次函数的关系式;
(2)求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点A0(1,0)作x轴的垂线,交直线l:y=2x于B1,在x轴上取点A1,使OA1=OB1,过点A1作x轴的垂线,交直线l于B2,在x轴上取点A2,使OA2=OB2,过点A2作x轴的垂线,交直线l于B3,…,这样依次作图,则点B8的纵坐标为( )
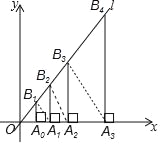
A. (
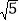 )7B. 2(
)7B. 2(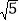 )7C. 2(
)7C. 2(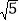 )8D. (
)8D. (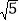 )9
)9
相关试题

