【题目】如图, ![]() 是⊙
是⊙ ![]() 的直径,
的直径, ![]() 、
、 ![]() 为⊙
为⊙ ![]() 上位于
上位于 ![]() 异侧的两点,连接
异侧的两点,连接 ![]() 并延长至点
并延长至点 ![]() ,使得
,使得 ![]() ,连接
,连接 ![]() 交⊙
交⊙ ![]() 于点
于点 ![]() ,连接
,连接 ![]() 、
、 ![]() 、
、 ![]() .
.
(1)证明: ![]() ;
;
(2)若 ![]() ,求
,求 ![]() 的度数;
的度数;
(3)设 ![]() 交
交 ![]() 于点
于点 ![]() ,若
,若 ![]() 是
是 ![]() 的中点,求
的中点,求 ![]() 的值.
的值.
参考答案:
【答案】
(1)证明:连接AD,

∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;
(2)解:∵四边形AEDF是⊙O的内接四边形,
∴∠AFD=180°-∠E,
又∵∠CFD=180°-∠AFD,
∴∠CFD=∠E=55°,
又∵∠E=∠C=55°,
∴∠BDF=∠C+∠CFD=110°
(3)解:连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=4,
在Rt△ABD中,cosB= ![]() ,BD=4,
,BD=4,
∴AB=6,
∵E是 ![]() 的中点,AB是⊙O的直径,
的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=3,
∴AE=3 ![]() ,
,
∵E是 ![]() 的中点,
的中点,
∴∠ADE=∠EAB,
∴△AEG∽△DEA,
∴ ![]() ,
,
即EGED=AE2=18
【解析】(1)由AB是⊙O的直径,得到AD⊥BC,CD=BD,得到AD垂直平分BC,根据垂直平分线的性质,线段垂直平分线上的点与线段的两个端点的距离相等,得到AB=AC,得到∠B=∠C,根据圆周角定理得到∠E=∠C;(2)由四边形AEDF是⊙O的内接四边形,得到∠AFD与∠E互补,又∠CFD与∠AFD互补,得到∠CFD=∠E,又∠E=∠C,∠BDF=∠C+∠CFD的度数;(3)根据在同一个圆中,等角所对的弦相等,得到FD=CD=BD,根据三角函数值,求出AB的值,由已知E是AB弧的中点,得到AE的值,和△AEG∽△DEA,得到比例,求出GED=AE2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、"10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2-6ax+4a+3的图像与y轴交于点A,点B是x轴上一点,其坐标为(1,0),连接AB,tan∠ABO=2.

(1)则点A的坐标为 , a=;
(2)过点A作AB的垂线与该二次函数的图像交于另一点C,求点C的坐标;
(3)连接BC,过点A作直线l交线段BC于点P,设点B、点C到l的距离分别为d1、d2 , 求d1+d2的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应“足球进校园”的号召,学校开设了足球兴趣拓展班,计划同时购买A,B两种足球30个,A,B两种足球的价格分别为50元
 个,80元
个,80元 个,设购买B种足球x个,购买两种足球的总费用为y元.
个,设购买B种足球x个,购买两种足球的总费用为y元. 求y关于x的函数表达式.
求y关于x的函数表达式. 在总费用不超过1600元的前提下,从节省费用的角度来考虑,求总费用的最小值.
在总费用不超过1600元的前提下,从节省费用的角度来考虑,求总费用的最小值. 因足球兴趣拓展班的人数增多,所以实际购买中这两种足球总数超过30个,总费用为2000元,则该学校可能共购买足球______个
因足球兴趣拓展班的人数增多,所以实际购买中这两种足球总数超过30个,总费用为2000元,则该学校可能共购买足球______个 直接写出答案
直接写出答案
-
科目: 来源: 题型:
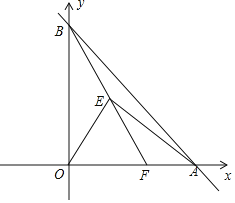
查看答案和解析>>【题目】如图,在直角坐标系中,直线
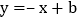 与x轴正半轴,y轴正半轴分别交于点A,B,点
与x轴正半轴,y轴正半轴分别交于点A,B,点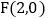 ,点E在第一象限,
,点E在第一象限,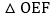 为等边三角形,连接AE,BE
为等边三角形,连接AE,BE 求点E的坐标;
求点E的坐标;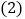 当BE所在的直线将
当BE所在的直线将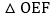 的面积分为3:1时,求
的面积分为3:1时,求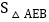 的面积;
的面积;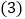 取线段AB的中点P,连接PE,OP,当
取线段AB的中点P,连接PE,OP,当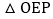 是以OE为腰的等腰三角形时,则
是以OE为腰的等腰三角形时,则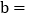 ______
______ 直接写出b的值
直接写出b的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次向右跳动至A1(-1,1),第二次向左跳动至A2(2,1),第三次向右跳动至A3(-2,2),第四次向左跳动至A4(3,2)依照此规律跳动下去,点A第2020次跳动至A2020的坐标为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 的图象与
的图象与  轴交于
轴交于  (1, 0),
(1, 0),  两点,与
两点,与  轴交于点
轴交于点  ,其顶点
,其顶点  的坐标为(-3, 2).
的坐标为(-3, 2).
(1)求这二次函数的关系式;
(2)求 的面积.
的面积.
相关试题

