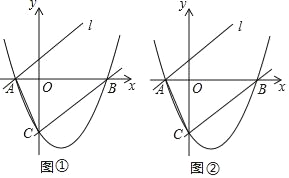
【题目】如图所示,抛物线y=![]() ﹣
﹣![]() x﹣4与x轴交于点A、B,与y 轴相交于点C.
x﹣4与x轴交于点A、B,与y 轴相交于点C.
(1)求直线BC的解析式;
(2)将直线BC向上平移后经过点A得到直线l:y=mx+n,点D在直线l上,若以A、B、C、D为顶点的四边形是平行四边形,求出点D的坐标.
参考答案:
【答案】(1)直线的解析式为y=![]() x﹣4;(2)点D的坐标为(4,4)或(﹣8,﹣4).
x﹣4;(2)点D的坐标为(4,4)或(﹣8,﹣4).
【解析】分析:(1)根据自变量与函数值得对应关系,可得A,B,C的坐标,根据待定系数法,可得答案;
(2)根据平行线的关系,可得m的值,根据待定系数法,可得n的值,根据勾股定理,可得AD,根据平行线的性质,可得关于x的方程,根据解方程,可得x值,再根据自变量与函数值得对应关系,可得D点坐标.
详解:(1)令y=0,得![]() x2-
x2-![]() x-4=0,
x-4=0,
解得:x1=-2,x2=6,
则得点A(-2,0),点B(6,0);
令x=0,得y=-4,
得点C(0,-4).
设直线BC的解析式为y=kx+b,由题意得:
![]() ,
,
解得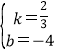 ,
,
∴直线的解析式为y=![]() x-4;
x-4;
(2)由将直线BC向上平移后经过点A得到直线:y=mx+n,
∴m=![]() ,
,
即y=![]() x+n,则
x+n,则![]() ×(-2)+n=0,
×(-2)+n=0,
∴n=![]() ,
,
则直线的解析式为:y=![]() x+
x+![]() ,
,
若以A、B、C、D为顶点的四边形是平行四边形,又AD∥BC,
∴AD=BC.
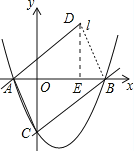
∵点在直线l上,设点D的坐标为(x,![]() x+
x+![]() ),过点D作DE⊥AB于E,
),过点D作DE⊥AB于E,
则AE2+DE2=AD2,又AD=BC![]() ,
,
∴(x+2)2+(![]() x+
x+![]() )2=52,
)2=52,
解得:x1=4,x2=-8.
当x=4时,![]() x+
x+![]() =4;
=4;
当x=-8时,![]() x+
x+![]() =-4,
=-4,
故点D的坐标为(4,4)或(-8,-4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①abc>0;②4ac﹣b2<0;③4a+c<2b;④3b+2c<0;⑤m(am+b)+b<a(m≠﹣1).其中结论正确的个数是( )
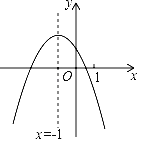
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有数字1、2、3的蓝色卡片,卡片除颜色和数字外完全相同.
(1)从中任意抽取一张卡片,求该卡片上写有数字2的概率;
(2)将三张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成个两位数,求这个两位数大于30的概率.
-
科目: 来源: 题型:
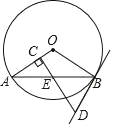
查看答案和解析>>【题目】如图所示,AB是⊙O的一条弦,DB切⊙O于点B,过点D作DC⊥OA于点C,DC与AB相交于点E.
(1)求证:DB=DE;
(2)若∠BDE=70°,求∠AOB的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题背景】
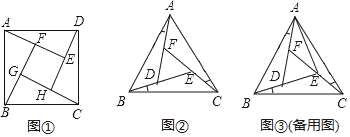
如图①所示,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
【类比研究】
如图②所示,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)连结AE,若AF=DF,AB=7,求△DEF的边长.
-
科目: 来源: 题型:
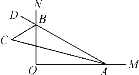
查看答案和解析>>【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上移动,∠OAB的平分线与∠OBA的外角平分线交于点C,试猜想:随着点A,B的移动,∠ACB的大小是否发生变化,并说明理由.
相关试题

