【题目】下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
参考答案:
【答案】A
【解析】
结合已知条件和全等三角形的判定方法,对所给的三个命题依次判定,即可解答..
①正确.可以用AAS或者ASA判定两个三角形全等;
②正确.
如图,分别延长AD,A′D′到E,E′,使得AD=DE,A′D′=D′E′,
∴△ADC≌△EDB,
∴BE=AC,
同理:B′E′=A′C′,
∴BE=B′E′,AE=A′E′,
∴△ABE≌△A′B′E′,
∴∠BAE=∠B′A′E′,∠E=∠E′,
∴∠CAD=∠C′A′D′,
∴∠BAC=∠B′A′C′,
∴△BAC≌△B′A′C′.
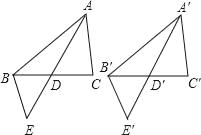
③不正确.因为这个高可能在三角形的内部,也有可能在三角形的外部,也就是说,这两个三角形可能一个是锐角三角形,一个是钝角三角形,所以就不全等了.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A的坐标为(﹣2,0),直线y=﹣
 x+3与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A、B、C三点.
x+3与x轴、y轴分别交于点B和点C,连接AC,顶点为D的抛物线y=ax2+bx+c过A、B、C三点. 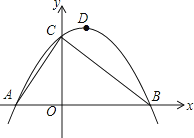
(1)请直接写出B、C两点的坐标,抛物线的解析式及顶点D的坐标;
(2)设抛物线的对称轴DE交线段BC于点E,P是第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标;
(3)设点M是线段BC上的一动点,过点M作MN∥AB,交AC于点N,点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t(秒),当t(秒)为何值时,存在△QMN为等腰直角三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题
大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,但是由于
的小数部分我们不可能全部地写出来,但是由于 ,所以
,所以 的整数部分为1,将
的整数部分为1,将 减去其整数部分1,所得的差就是其小数部分
减去其整数部分1,所得的差就是其小数部分 ,根据以上的内容,解答下面的问题:
,根据以上的内容,解答下面的问题: 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______; 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______; 整数部分是______,小数部分是______;
整数部分是______,小数部分是______; 若设
若设 整数部分是x,小数部分是y,求
整数部分是x,小数部分是y,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC经过一次平移到△DFE的位置,请回答下列问题:

(1)点C的对应点是点__________,∠D=__________,BC=__________;
(2)连接CE,那么平移的方向就是__________的方向,平移的距离就是线段__________的长度;
(3)连接AD,BF,BE,与线段CE相等的线段有__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知图1将线段AB向右平移1个单位长度,图2是将线段AB折一下再向右平移1个单位长度,请在图3中画出一条有两个折点的折线向右平移1个单位长度的图形;

(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩下部分的面积;
(3)如图4,在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽度为1 m,求这块菜地的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( )

A.1 B.2 C.5 D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=
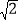 ﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )
﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

