【题目】已知直线l1:y=﹣ ![]() 与直线l2:y=kx﹣
与直线l2:y=kx﹣ ![]() 交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.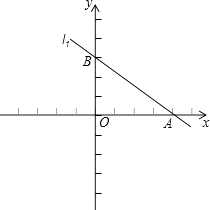
(1)求k的值,并作出直线l2图象;
(2)若点P是线段AB上的点且△ACP的面积为15,求点P的坐标;
(3)若点M、N分别是x轴上、线段AC上的动点(点M不与点O重合),是否存在点M、N,使得△ANM≌△AOC?若存在,请求出N点的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵直线l1:y=﹣ ![]() x+3与x轴交于点A,
x+3与x轴交于点A,
∴令y=0时,x=4,即A(4,0),
将A(4,0)代入直线l2:y=kx﹣ ![]() ,得k=
,得k= ![]() ,
,
直线l2图象如图1所示;
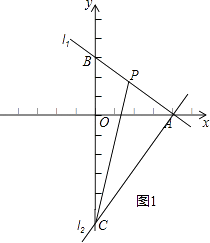
(2)解:设P(a,b),
根据题意得:S△ACP=S△ABC﹣S△PBC= ![]() ×(3+
×(3+ ![]() )×4﹣
)×4﹣ ![]() ×(3+
×(3+ ![]() )a=15,
)a=15,
解得:a= ![]() ,
,
将P( ![]() ,b)代入直线l1得:b=
,b)代入直线l1得:b= ![]() ×(﹣
×(﹣ ![]() )+3=﹣
)+3=﹣ ![]() +3=
+3= ![]() ,
,
∴点P的坐标( ![]() ,
, ![]() )
)
(3)解:如图2,作ND⊥x轴于D,
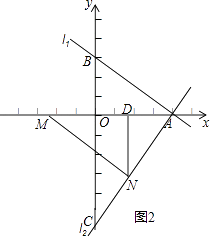
∵AC= ![]() =
= ![]() ,△ANM≌△AOC,
,△ANM≌△AOC,
∴AM=AC= ![]() ,AN=AO=4,MN=OC=
,AN=AO=4,MN=OC= ![]() ,∠ANM=∠AOC=90°,
,∠ANM=∠AOC=90°,
∵S△AMN= ![]() AMND=
AMND= ![]() ANMN,
ANMN,
∴ND= ![]() =
= ![]() =
= ![]() ,
,
将N的纵坐标y=﹣ ![]() 代入直线l2得:x=
代入直线l2得:x= ![]() ,
,
∴当N的纵坐标为( ![]() ,﹣
,﹣ ![]() )时,△ANM≌△AOC
)时,△ANM≌△AOC
【解析】(1)对于直线l1,令y=0求出x的值,确定出A坐标,代入直线l2求出k的值,作出直线l2图象即可;
(2)设P(a,b),由S△ACP=S△ABC-S△BPC,求出a的值,进而求出b的值,确定出P坐标即可;
(3)如图2,作ND⊥x轴于D,利用勾股定理求出AC的长,由△ANM≌△AOC,得到对应边相等,表示出AM,AN,MN,确定出△AMN为直角三角形,利用面积法求出ND的长,确定出N纵坐标,进而求出横坐标,确定出N坐标即可.
【考点精析】本题主要考查了确定一次函数的表达式和全等三角形的性质的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P位于x轴下方,距离x轴5个单位,位于y轴右方,距离y轴3个单位,那么P点的坐标是( )
A.(5,-3) B.(3,-5) C.(-5,3) D.(-3,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次捐款活动中,7位同学的捐款金额分别是5元,6元,6元,7元,8元,9元,10元,则这组数据的中位数与众数分别是( )
A.6,6
B.7,6
C.7,8
D.6,8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形
是等边三角形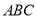 内一点,将线段
内一点,将线段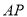 绕点
绕点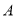 顺时针旋转60°得到线段
顺时针旋转60°得到线段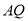 ,连接
,连接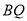 .若
.若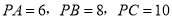 ,则四边形
,则四边形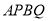 的面积为____.
的面积为____.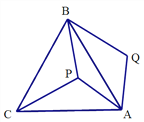
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下各组线段为边,能组成三角形的是( )
A. 8cm,6cm,4cm B. 2cm,4cm,6cm
C. 14cm,6cm,7cm D. 2cm,3cm,6cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC,在△ABC的外部作∠ACM,使得∠ACM=
 ∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.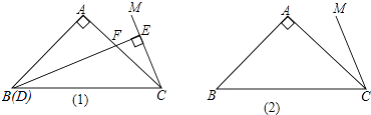
(1)如图1所示,当点D与点B重合时,延长BA,CM交点N,证明:DF=2EC;
(2)当点D在直线BC上运动时,DF和EC是否始终保持上述数量关系呢?请你在图2中画出点D运动到CB延长线上某一点时的图形,并证明此时DF与EC的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x
1
2
5
10
20
舒适度指数y
100
50
20
10
5
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
相关试题

