【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
参考答案:
【答案】(1)y=![]() (0<x≤30);(2)12.5;(3) 最多等待10分钟.
(0<x≤30);(2)12.5;(3) 最多等待10分钟.
【解析】试题分析: (1)观察表格发现:1×100=2×50=5×20,从而确定函数关系式y=![]() ,y代表舒适度指数,x(分)代表等待时间.
,y代表舒适度指数,x(分)代表等待时间.
(2)是已知x=8,代入函数解析式求得y.
(3)是已知y≥10,就可以得到关于x的不等式求的x的范围.
试题解析:
(1)观察表格发现:1×100=2×50=5×20=…,
∴xy=100,
∴y=![]() (0<x≤30);
(0<x≤30);
(2)当x=8时,舒适度y=![]() =12.5;
=12.5;
(3)舒适度指数不低于10时,由图象y≥10时,0<x≤10
所以作为食堂的管理员,让每个在窗口买菜的同学最多等待10分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=﹣
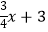 与直线l2:y=kx﹣
与直线l2:y=kx﹣ 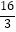 交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.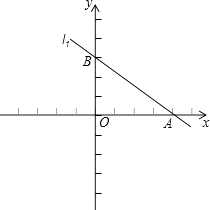
(1)求k的值,并作出直线l2图象;
(2)若点P是线段AB上的点且△ACP的面积为15,求点P的坐标;
(3)若点M、N分别是x轴上、线段AC上的动点(点M不与点O重合),是否存在点M、N,使得△ANM≌△AOC?若存在,请求出N点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下各组线段为边,能组成三角形的是( )
A. 8cm,6cm,4cm B. 2cm,4cm,6cm
C. 14cm,6cm,7cm D. 2cm,3cm,6cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC,在△ABC的外部作∠ACM,使得∠ACM=
 ∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.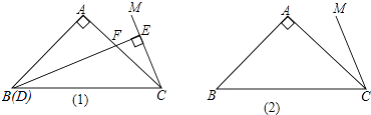
(1)如图1所示,当点D与点B重合时,延长BA,CM交点N,证明:DF=2EC;
(2)当点D在直线BC上运动时,DF和EC是否始终保持上述数量关系呢?请你在图2中画出点D运动到CB延长线上某一点时的图形,并证明此时DF与EC的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】地球上的海洋面积约为36105.9万平方千米,用科学记数法(保留三个有效数字)表示为平方千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列三角形中:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角形.其中是等边三角形的有( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=x﹣
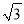 与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=
与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=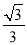 x2+bx+c经过点B(﹣1,0)和点C.
x2+bx+c经过点B(﹣1,0)和点C.(1)填空:直接写出抛物线的解析式:_____;
(2)已知点Q是抛物线y=
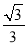 x2+bx+c在第四象限内的一个动点.
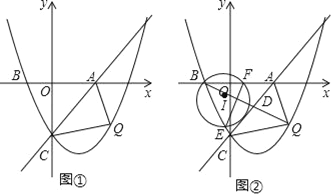
x2+bx+c在第四象限内的一个动点.①如图,连接AQ、CQ,设点Q的横坐标为t,△AQC的面积为S,求S与t的函数关系式,并求出S的最大值;
②连接BQ交AC于点D,连接BC,以BD为直径作⊙I,分别交BC、AB于点E、F,连接EF,求线段EF的最小值,并直接写出此时Q点的坐标.
相关试题

