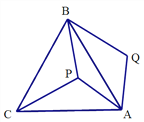
【题目】如图, ![]() 是等边三角形
是等边三角形![]() 内一点,将线段
内一点,将线段![]() 绕点
绕点![]() 顺时针旋转60°得到线段
顺时针旋转60°得到线段![]() ,连接
,连接![]() .若
.若![]() ,则四边形
,则四边形![]() 的面积为____.
的面积为____.
参考答案:
【答案】24+9![]() .
.
【解析】试题分析:如图,连结PQ,根据等边三角形的性质得∠BAC=60°,AB=AC,再根据旋转的性质得AP=PQ=6,∠PAQ=60°,即可判定△APQ为等边三角形,所以PQ=AP=6;在△APC和△ABQ中,AB=AC,∠CAP=∠BAQ,AP=PQ,利用SAS判定△APC≌△ABQ,根据全等三角形的性质可得PC=QB=10;在△BPQ中,已知PB2=82=64,PQ2=62,BQ2=102,即PB2+PQ2=BQ2,所以△PBQ为直角三角形,∠BPQ=90°,所以S四边形APBQ=S△BPQ+S△APQ=![]() ×6×8
×6×8![]() +×62=24+9
+×62=24+9![]() .
.
-
科目: 来源: 题型:
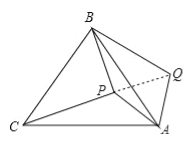
查看答案和解析>>【题目】把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s).
(1)用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;
(2)连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;
(3)当t为何值时,△APQ是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P位于x轴下方,距离x轴5个单位,位于y轴右方,距离y轴3个单位,那么P点的坐标是( )
A.(5,-3) B.(3,-5) C.(-5,3) D.(-3,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次捐款活动中,7位同学的捐款金额分别是5元,6元,6元,7元,8元,9元,10元,则这组数据的中位数与众数分别是( )
A.6,6
B.7,6
C.7,8
D.6,8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=﹣
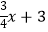 与直线l2:y=kx﹣
与直线l2:y=kx﹣ 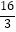 交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.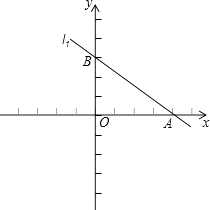
(1)求k的值,并作出直线l2图象;
(2)若点P是线段AB上的点且△ACP的面积为15,求点P的坐标;
(3)若点M、N分别是x轴上、线段AC上的动点(点M不与点O重合),是否存在点M、N,使得△ANM≌△AOC?若存在,请求出N点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下各组线段为边,能组成三角形的是( )
A. 8cm,6cm,4cm B. 2cm,4cm,6cm
C. 14cm,6cm,7cm D. 2cm,3cm,6cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC,在△ABC的外部作∠ACM,使得∠ACM=
 ∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.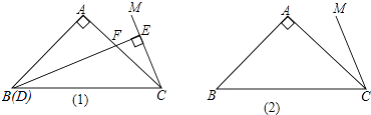
(1)如图1所示,当点D与点B重合时,延长BA,CM交点N,证明:DF=2EC;
(2)当点D在直线BC上运动时,DF和EC是否始终保持上述数量关系呢?请你在图2中画出点D运动到CB延长线上某一点时的图形,并证明此时DF与EC的数量关系.
相关试题

