【题目】在△ABC中,∠BAC=90°,AB=AC,在△ABC的外部作∠ACM,使得∠ACM= ![]() ∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.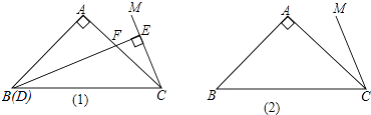
(1)如图1所示,当点D与点B重合时,延长BA,CM交点N,证明:DF=2EC;
(2)当点D在直线BC上运动时,DF和EC是否始终保持上述数量关系呢?请你在图2中画出点D运动到CB延长线上某一点时的图形,并证明此时DF与EC的数量关系.
参考答案:
【答案】
(1)解:如图(1),延长BA,CM交点N,

∵∠A=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵∠ACM= ![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠BCM=67.5°,
∴∠BNC=67.5°=∠BCM,
∴BC=BN,
∵BE⊥CE,
∴∠ABE=22.5°,CN=2CE,
∴∠ABE=∠ACM=22.5°,
在△BAF和△CAN中, 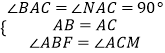 ,
,
∴△BAF≌△CAN(ASA),
∴BF=CN,
∴BF=2CE
(2)解:保持上述关系;BF=2CE;
证明如下:
作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,
如图(2)所示:
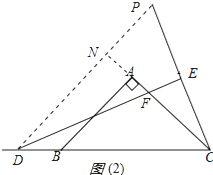
∵DE⊥PC,∠ECD=67.5,
∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°,
∴PD=CD,
∴PE=EC,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD=∠NDC,∠DNC=90°,
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中, 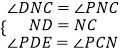 ,
,
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE.
【解析】(1)延长BA,CM交点N,先证明BC=BN,得出CN=2CE,再证明△BAF≌△CAN,得出对应边相等BF=CN,即可得出结论;
(2)作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,先证明PD=CD,得出PC=2CE,再证明△DNF≌△PNC,得出对应边相等DF=PC,即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
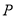 是等边三角形
是等边三角形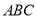 内一点,将线段
内一点,将线段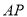 绕点
绕点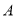 顺时针旋转60°得到线段
顺时针旋转60°得到线段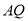 ,连接
,连接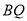 .若
.若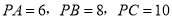 ,则四边形
,则四边形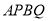 的面积为____.
的面积为____.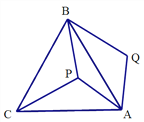
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=﹣
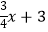 与直线l2:y=kx﹣
与直线l2:y=kx﹣ 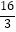 交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.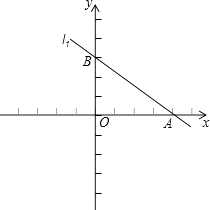
(1)求k的值,并作出直线l2图象;
(2)若点P是线段AB上的点且△ACP的面积为15,求点P的坐标;
(3)若点M、N分别是x轴上、线段AC上的动点(点M不与点O重合),是否存在点M、N,使得△ANM≌△AOC?若存在,请求出N点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下各组线段为边,能组成三角形的是( )
A. 8cm,6cm,4cm B. 2cm,4cm,6cm
C. 14cm,6cm,7cm D. 2cm,3cm,6cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x
1
2
5
10
20
舒适度指数y
100
50
20
10
5
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球上的海洋面积约为36105.9万平方千米,用科学记数法(保留三个有效数字)表示为平方千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列三角形中:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角形.其中是等边三角形的有( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
相关试题

