【题目】某游泳馆普通票价30元![]() 张,暑假为了促销,新推出一种优惠卡:售价300元
张,暑假为了促销,新推出一种优惠卡:售价300元![]() 张,每次凭卡另收15元
张,每次凭卡另收15元![]() 暑假普通票正常出售,优惠卡仅限暑假使用,不限次数
暑假普通票正常出售,优惠卡仅限暑假使用,不限次数![]() 设游泳x次时,所需总费用为y元.
设游泳x次时,所需总费用为y元.
![]() 分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式;
分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式;
![]() 在同一坐标系中,若两种消费方式对应的函数图象如图所示,请求出点A、B的坐标;
在同一坐标系中,若两种消费方式对应的函数图象如图所示,请求出点A、B的坐标;

参考答案:
【答案】(1) y=300+15x ,y=30x ;(2) A(0,300),B(20,600).
【解析】
![]() 根据题意可以分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式;
根据题意可以分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式;
![]() 根据题意可知,点A的坐标就是选择优惠卡时对应的函数解析式与y轴的交点,点B的坐标就是两个函数交点的坐标,本题得以解决.
根据题意可知,点A的坐标就是选择优惠卡时对应的函数解析式与y轴的交点,点B的坐标就是两个函数交点的坐标,本题得以解决.
解:![]() 由题意可得,
由题意可得,
选择优惠卡时,y与x的函数关系式为:![]() ,
,
当选择普通票时,y与x的函数关系式为:![]() ;
;
![]() 将
将![]() 代入
代入![]() ,得
,得![]() ,即点A的坐标为
,即点A的坐标为![]() ,
,
令![]() ,得
,得![]() ,则
,则![]() ,即点B的坐标为
,即点B的坐标为![]() ,
,
由上可得,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() .
.
故答案为:(1) y=300+15x,y=30x ;(2) A(0,300),B(20,600).
-
科目: 来源: 题型:
查看答案和解析>>【题目】请将下列证明过程补充完整:
已知:如图,AE平分∠BAC,CE平分∠ACD,且∠α+∠β=90°.
求证:AB∥CD.
证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α(______________________)
∵AE平分∠BAC (已知),
∴∠BAC=_________(______________________)
∵∠α+∠β=90°(已知),
∴2∠α+2∠β=180°(等式的性质)
∴∠ACD+∠BAC==_________(______________________)
∴AB∥CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角板如图摆放,点F是 45°角三角板△ABC的斜边的中点,AC=4.当 30°角三角板DEF的直角顶点绕着点F旋转时,直角边DF,EF分别与AC,BC相交于点 M, N.在旋转过程中有以下结论:①MF=NF;②CF与MN可能相等吗;③MN 长度的最小值为 2;④四边形CMFN的面积保持不变; ⑤△CMN面积的最大值为 2.其中正确的个数是_________.(填写序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一小球从斜坡D点处抛出,球的抛出路线可以用二次函数)y=-x2+4x刻画,斜坡OA可以用一次函数y=
 刻画.
刻画.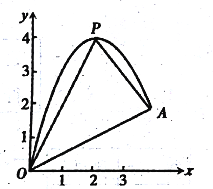
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积,请直接写出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图
 是我们常见的基本图形,我们可以称之为“8”字形
是我们常见的基本图形,我们可以称之为“8”字形 “8”字形有一个重要的性质如下:
“8”字形有一个重要的性质如下: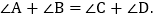 利用这个性质并结合你所学的知识解决以下问题:
利用这个性质并结合你所学的知识解决以下问题: 如图
如图 ,
,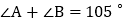 ,
,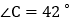 ,直接写出
,直接写出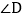 的度数为______;
的度数为______;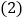 如图
如图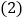 ,若BN、DN分别是
,若BN、DN分别是 、
、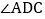 的角平分线,BN与DN交于点N、且
的角平分线,BN与DN交于点N、且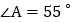 ,
,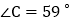 ,求
,求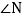 的度数;
的度数; 如图
如图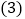 ,若AM、BN、CM、DN分别是
,若AM、BN、CM、DN分别是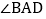 、
、 、
、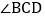 和
和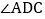 的角平分线,AM与CM、BN交于点M、G,DN与BN、CM交于点N、H,且
的角平分线,AM与CM、BN交于点M、G,DN与BN、CM交于点N、H,且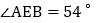 ,求
,求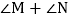 的度数.
的度数.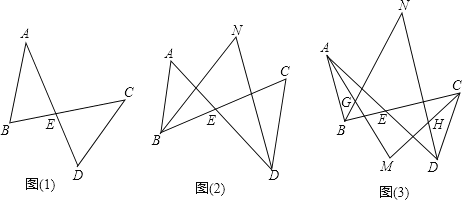
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
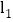 :
: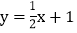 和直线
和直线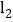 :
: ,过点
,过点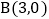 作
作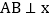 轴,交直线
轴,交直线 于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与
于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与 、
、 交于点C、D,连接AD、BC.
交于点C、D,连接AD、BC.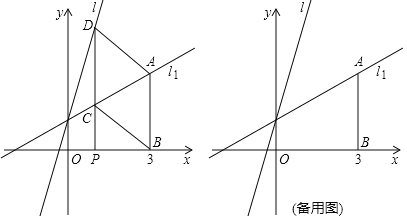
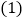 直接写出线段
直接写出线段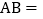 ______;
______;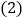 当P的坐标是
当P的坐标是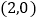 时,求直线BC的解析式;
时,求直线BC的解析式; 若
若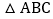 的面积与
的面积与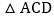 的面积相等,求点P的坐标.
的面积相等,求点P的坐标. -
科目: 来源: 题型:
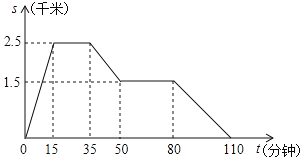
查看答案和解析>>【题目】一天,王亮同学从家里跑步到体育馆,在那里锻炼了一阵后又走到某书店去买书, 然后散步走回家如图反映的是在这一过程中,王亮同学离家的距离 s(千米)与离家的时间 t(分钟)之间的关系,请根据图象解答下列问题:
(1)体育馆离家的距离为 千米,书店离家的距离为_____千米;王亮同学在书店待了______分钟.
(2)分别求王亮同学从体育馆走到书店的平均速度和从书店出来散步回家的平均速度.
相关试题

