【题目】如图,一小球从斜坡D点处抛出,球的抛出路线可以用二次函数)y=-x2+4x刻画,斜坡OA可以用一次函数y=![]() 刻画.
刻画.
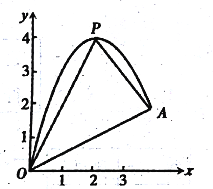
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积,请直接写出点M的坐标.
参考答案:
【答案】(1)P(2,4);(2)A(![]() ,
, ![]() );(3)
);(3)![]() ;(4)M(
;(4)M(![]() ,
, ![]() ).
).
【解析】试题分析:(1)利用配方法抛物线的一般式化为顶点式,即可求出二次函数图象的最高点P的坐标;
(2)联立两解析式,可求出交点A的坐标;
(3)作PQ⊥x轴于点Q,AB⊥x轴于点B.根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA,代入数值计算即可求解;
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,由于两平行线之间的距离相等,根据同底等高的两个三角形面积相等,可得△MOA的面积等于△POA的面积.设直线PM的解析式为y=![]() x+b,将P(2,4)代入,求出直线PM的解析式为y=
x+b,将P(2,4)代入,求出直线PM的解析式为y=![]() x+3.再与抛物线的解析式联立,得到方程组
x+3.再与抛物线的解析式联立,得到方程组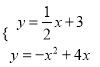 ,解方程组即可求出点M的坐标.
,解方程组即可求出点M的坐标.
试题解析:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,
故二次函数图象的最高点P的坐标为(2,4);
(2)联立两解析式可得: 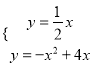 ,解得:
,解得: ![]() ,或
,或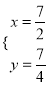 .
.
故可得点A的坐标为(![]() ,
, ![]() );
);
(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.
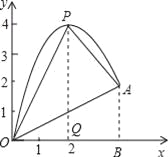
S△POA=S△POQ+S△梯形PQBA﹣S△BOA
=![]() ×2×4+
×2×4+![]() ×(
×(![]() +4)×(
+4)×(![]() ﹣2)﹣
﹣2)﹣![]() ×
×![]() ×
×![]()
=4+![]() ﹣
﹣![]()
=![]() ;
;
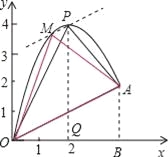
(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.
设直线PM的解析式为y=![]() x+b,
x+b,
∵P的坐标为(2,4),
∴4=![]() ×2+b,解得b=3,
×2+b,解得b=3,
∴直线PM的解析式为y=![]() x+3.
x+3.
由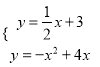 ,解得
,解得![]() ,
, 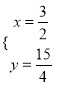 ,
,
∴点M的坐标为(![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校八年级体育科目训练情况,从八年级学生中随机抽取了部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图
 请根据统计图中的信息解答下列问题:
请根据统计图中的信息解答下列问题:
(1)图1中
 的度数是__________,并把图2条形统计图补充完整.
的度数是__________,并把图2条形统计图补充完整.(2)抽取的这部分的学生的体育科目测试结果的中位数是在__________级;
(3)依次将优秀、良好、及格、不及格记为90分、80分、70分、50分,请计算抽取的这部分学生体育的平均成绩.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请将下列证明过程补充完整:
已知:如图,AE平分∠BAC,CE平分∠ACD,且∠α+∠β=90°.
求证:AB∥CD.
证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α(______________________)
∵AE平分∠BAC (已知),
∴∠BAC=_________(______________________)
∵∠α+∠β=90°(已知),
∴2∠α+2∠β=180°(等式的性质)
∴∠ACD+∠BAC==_________(______________________)
∴AB∥CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角板如图摆放,点F是 45°角三角板△ABC的斜边的中点,AC=4.当 30°角三角板DEF的直角顶点绕着点F旋转时,直角边DF,EF分别与AC,BC相交于点 M, N.在旋转过程中有以下结论:①MF=NF;②CF与MN可能相等吗;③MN 长度的最小值为 2;④四边形CMFN的面积保持不变; ⑤△CMN面积的最大值为 2.其中正确的个数是_________.(填写序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某游泳馆普通票价30元
 张,暑假为了促销,新推出一种优惠卡:售价300元
张,暑假为了促销,新推出一种优惠卡:售价300元 张,每次凭卡另收15元
张,每次凭卡另收15元 暑假普通票正常出售,优惠卡仅限暑假使用,不限次数
暑假普通票正常出售,优惠卡仅限暑假使用,不限次数 设游泳x次时,所需总费用为y元.
设游泳x次时,所需总费用为y元. 分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式;
分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式; 在同一坐标系中,若两种消费方式对应的函数图象如图所示,请求出点A、B的坐标;
在同一坐标系中,若两种消费方式对应的函数图象如图所示,请求出点A、B的坐标;
-
科目: 来源: 题型:
查看答案和解析>>【题目】图
 是我们常见的基本图形,我们可以称之为“8”字形
是我们常见的基本图形,我们可以称之为“8”字形 “8”字形有一个重要的性质如下:
“8”字形有一个重要的性质如下: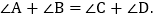 利用这个性质并结合你所学的知识解决以下问题:
利用这个性质并结合你所学的知识解决以下问题: 如图
如图 ,
,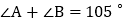 ,
,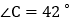 ,直接写出
,直接写出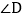 的度数为______;
的度数为______;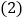 如图
如图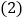 ,若BN、DN分别是
,若BN、DN分别是 、
、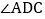 的角平分线,BN与DN交于点N、且
的角平分线,BN与DN交于点N、且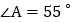 ,
,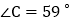 ,求
,求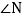 的度数;
的度数; 如图
如图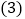 ,若AM、BN、CM、DN分别是
,若AM、BN、CM、DN分别是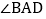 、
、 、
、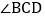 和
和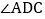 的角平分线,AM与CM、BN交于点M、G,DN与BN、CM交于点N、H,且
的角平分线,AM与CM、BN交于点M、G,DN与BN、CM交于点N、H,且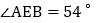 ,求
,求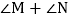 的度数.
的度数.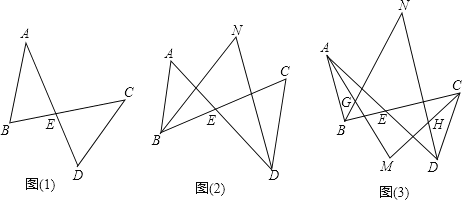
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
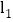 :
: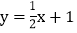 和直线
和直线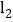 :
: ,过点
,过点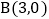 作
作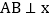 轴,交直线
轴,交直线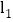 于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与
于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与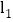 、
、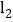 交于点C、D,连接AD、BC.
交于点C、D,连接AD、BC.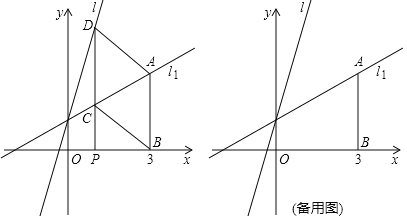
 直接写出线段
直接写出线段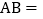 ______;
______; 当P的坐标是
当P的坐标是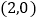 时,求直线BC的解析式;
时,求直线BC的解析式; 若
若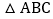 的面积与
的面积与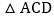 的面积相等,求点P的坐标.
的面积相等,求点P的坐标.
相关试题

