【题目】如图,已知直线![]() :
:![]() 和直线
和直线![]() :
:![]() ,过点
,过点![]() 作
作![]() 轴,交直线
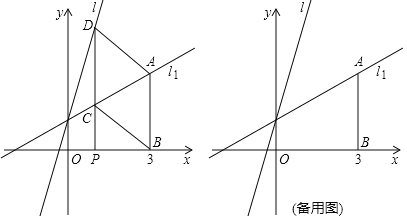
轴,交直线![]() 于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与
于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与![]() 、
、![]() 交于点C、D,连接AD、BC.
交于点C、D,连接AD、BC.
![]() 直接写出线段
直接写出线段![]() ______;
______;
![]() 当P的坐标是
当P的坐标是![]() 时,求直线BC的解析式;
时,求直线BC的解析式;
![]() 若
若![]() 的面积与
的面积与![]() 的面积相等,求点P的坐标.
的面积相等,求点P的坐标.
参考答案:
【答案】(1) ![]() ;(2) y=-2x+4; (3) (1,0)或(-1,0).
;(2) y=-2x+4; (3) (1,0)或(-1,0).
【解析】
![]() 轴
轴![]() 且点A在直线
且点A在直线![]() 上,点B的坐标为
上,点B的坐标为![]() 所以求出点A的坐标即可求AB;
所以求出点A的坐标即可求AB;
![]() 因
因![]() 轴于点P,点
轴于点P,点![]() ,点C在直线
,点C在直线![]() 上,即可以求出点C的坐标,即可用待定系数法求直线BC的解析式;
上,即可以求出点C的坐标,即可用待定系数法求直线BC的解析式;
![]() 因
因![]() 的面积与
的面积与![]() 的面积相等,即
的面积相等,即![]() 时两三角形的面积相等,设点
时两三角形的面积相等,设点![]() ,则有
,则有![]() ,即可求出点P的坐标.
,即可求出点P的坐标.
解:![]() 轴
轴![]() 且点A在直线
且点A在直线![]() 上,
上,
![]() 将
将![]() 代入
代入![]() ,得
,得![]() ,
,
即![]() ;
;
![]() 点
点![]() 轴,
轴,
![]() 将
将![]() 代入
代入![]() ,得
,得![]() ,故点C的坐标为
,故点C的坐标为![]() ,
,
设直线BC的解析式为:![]() ,将点C,点B代入得:
,将点C,点B代入得:
![]() ,解得
,解得![]() ,
,
故直线BC的解析式为:![]() ;
;
![]() 由题意得,当
由题意得,当![]() 时,
时,![]() ,
,
设点P的坐标为![]() ,
,
![]() ,解得
,解得![]() 或
或![]() .
.
![]() 点P的坐标为
点P的坐标为![]() 或
或![]() .
.
故答案为:(1) ![]() ;(2) y=-2x+4;(3) (1,0)或(-1,0).
;(2) y=-2x+4;(3) (1,0)或(-1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一小球从斜坡D点处抛出,球的抛出路线可以用二次函数)y=-x2+4x刻画,斜坡OA可以用一次函数y=
 刻画.
刻画.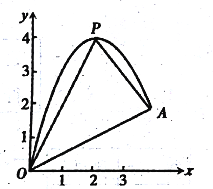
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积,请直接写出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游泳馆普通票价30元
 张,暑假为了促销,新推出一种优惠卡:售价300元
张,暑假为了促销,新推出一种优惠卡:售价300元 张,每次凭卡另收15元
张,每次凭卡另收15元 暑假普通票正常出售,优惠卡仅限暑假使用,不限次数
暑假普通票正常出售,优惠卡仅限暑假使用,不限次数 设游泳x次时,所需总费用为y元.
设游泳x次时,所需总费用为y元. 分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式;
分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式; 在同一坐标系中,若两种消费方式对应的函数图象如图所示,请求出点A、B的坐标;
在同一坐标系中,若两种消费方式对应的函数图象如图所示,请求出点A、B的坐标;
-
科目: 来源: 题型:
查看答案和解析>>【题目】图
 是我们常见的基本图形,我们可以称之为“8”字形
是我们常见的基本图形,我们可以称之为“8”字形 “8”字形有一个重要的性质如下:
“8”字形有一个重要的性质如下: 利用这个性质并结合你所学的知识解决以下问题:
利用这个性质并结合你所学的知识解决以下问题: 如图
如图 ,
,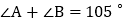 ,
,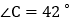 ,直接写出
,直接写出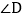 的度数为______;
的度数为______; 如图
如图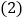 ,若BN、DN分别是
,若BN、DN分别是 、
、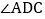 的角平分线,BN与DN交于点N、且
的角平分线,BN与DN交于点N、且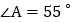 ,
,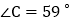 ,求
,求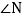 的度数;
的度数;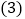 如图
如图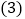 ,若AM、BN、CM、DN分别是
,若AM、BN、CM、DN分别是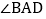 、
、 、
、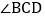 和
和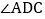 的角平分线,AM与CM、BN交于点M、G,DN与BN、CM交于点N、H,且
的角平分线,AM与CM、BN交于点M、G,DN与BN、CM交于点N、H,且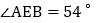 ,求
,求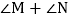 的度数.
的度数.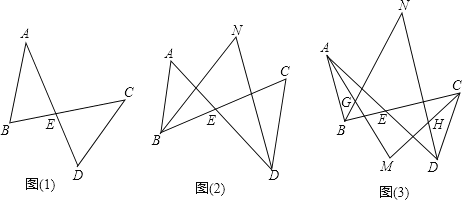
-
科目: 来源: 题型:
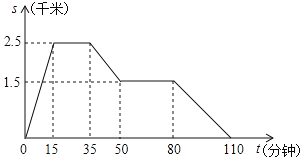
查看答案和解析>>【题目】一天,王亮同学从家里跑步到体育馆,在那里锻炼了一阵后又走到某书店去买书, 然后散步走回家如图反映的是在这一过程中,王亮同学离家的距离 s(千米)与离家的时间 t(分钟)之间的关系,请根据图象解答下列问题:
(1)体育馆离家的距离为 千米,书店离家的距离为_____千米;王亮同学在书店待了______分钟.
(2)分别求王亮同学从体育馆走到书店的平均速度和从书店出来散步回家的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某课外活动小组为了了解本校学生上网目的,随机调查了本校的部分学生,根据调查结果,统计整理并制作了如下尚不完整的统计图,根据以上信息解答下列问题:
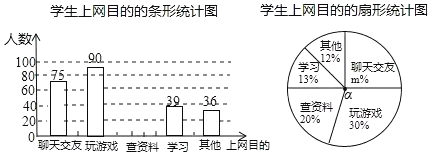
(1)参与本次调查的学生共有_____人;
(2)在扇形统计图中,m的值为_____;圆心角α=_____度.
(3)补全条形统计图;
(4)中学生上网玩游戏、聊天交友已经对正常的学习产生较多负面影响,为此学校计划开展一次“合理上网”专题讲座,每班随机抽取15名学生参加,小明所在的班级有50名学生,他被抽到听讲座的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
相关试题

