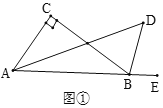
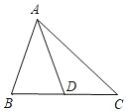
【题目】(1)如图①,在△ABC中,∠C=90°,∠BAC的平分线与外角∠CBE的平分线相交于点D,求∠D的度数.
(2)如图②,将(1)中的条件“![]() ”改为
”改为![]() ,其它条件不变,请直接写出
,其它条件不变,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由三角形外角的性质,可得∠C=∠CBE-∠CAB,∠D=∠2-∠1,又由∠BAC的平分线与外角∠CBE的平分线相交于点D,根据角平分线的性质,可得∠1=![]() ∠CAB,∠2=
∠CAB,∠2=![]() ∠CBE,继而可求得答案;
∠CBE,继而可求得答案;
(2)根据(1)的方法进行推导即可得答案.
(1)∵∠CBE是△ABC的外角,
∴∠CBE=∠CAB+∠C,
∴∠C=∠CBE-∠CAB,
∵∠BAC的平分线与外角∠CBE的平分线相交于点D,
∴∠1=![]() ∠CAB,∠2=
∠CAB,∠2=![]() ∠CBE,
∠CBE,
∵∠2是△ABD的外角,
∴∠2=∠1+∠D,
∴∠D=∠2-∠1=![]() (∠CBE-∠CAB)=
(∠CBE-∠CAB)=![]() ∠C=
∠C=![]() ×90°=45°;
×90°=45°;
(2)![]() ,理由如下:
,理由如下:
∵∠CBE是△ABC的外角,
∴∠CBE=∠CAB+∠C,
∴∠C=∠CBE-∠CAB,
∵∠BAC的平分线与外角∠CBE的平分线相交于点D,
∴∠1=![]() ∠CAB,∠2=
∠CAB,∠2=![]() ∠CBE,
∠CBE,
∵∠2是△ABD的外角,
∴∠2=∠1+∠D,
∴∠D=∠2-∠1=![]() (∠CBE-∠CAB)=
(∠CBE-∠CAB)=![]() ∠C=
∠C=![]() α.
α.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形ABCD,AB=4,BC=
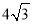 .
.(1)直接写出:∠ABD=______度;
(2)将矩形ABCD沿BD剪开得到两个三角形,按图2摆放:点A与点C重合,CD落在AD′上,直接写出BD与B′D′的关系:_____;
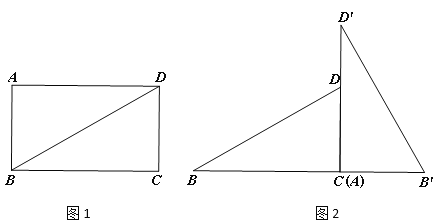
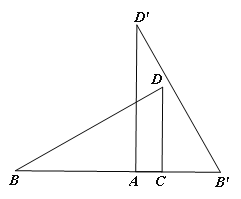
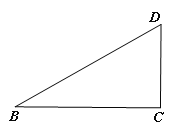
(3)在图2的基础上将△AB′D′向左平移,点B′与B重合停止,设AC=x,两个三角形重合部分的封闭图形的周长为y,请用x表示y:____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
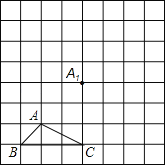
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,得到△A1B2C2,在网格中画出旋转后的△A1B2C2.
(3)连结
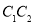 ,请判断
,请判断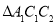 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
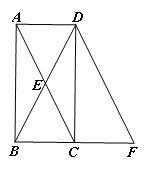
查看答案和解析>>【题目】如图所示,在△ABC 中,AD 是 BC 边上的中线.
(1)画出与△ACD 关于点 D 成中心对称的三角形;
(2)找出与 AC 相等的线段;
(3)探索:△ABC 中,AB+AC 与中线 AD 之间的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的对角线交于点E,将△DCB沿CD翻折得到△DCF.
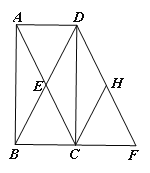
(1)求证:四边形ACFD是平行四边形;
(2)点H为DF的中点,连结CH,若AB=4,BC=2,求四边形ECHD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在10×10网格中,点A和直线l的位置如图所示:

(1)将点A向右平移6个单位,再向上平移2个单位长度得到点B,在网格中标出点B;
(2)在(1)的条件下,在直线l上确定一点P,使PA+PB的值最小,保留画图痕迹,并直接写出PA+PB的最小值:______;
(3)结合(2)的画图过程并思考,直接写出
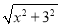 +
+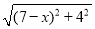 的最小值:____
的最小值:____
相关试题

