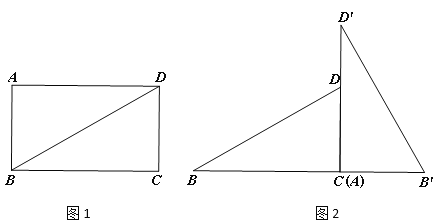
【题目】如图1,矩形ABCD,AB=4,BC=![]() .
.
(1)直接写出:∠ABD=______度;
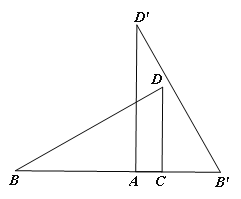
(2)将矩形ABCD沿BD剪开得到两个三角形,按图2摆放:点A与点C重合,CD落在AD′上,直接写出BD与B′D′的关系:_____;
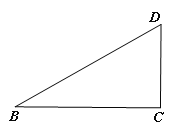
(3)在图2的基础上将△AB′D′向左平移,点B′与B重合停止,设AC=x,两个三角形重合部分的封闭图形的周长为y,请用x表示y:____.
参考答案:
【答案】60 BD=B′D′,BD⊥B′D′ 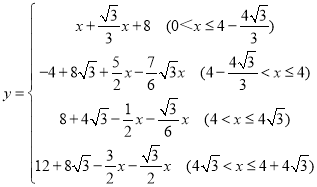
【解析】
(1)解直角三角形即可解决问题.
(2)结论:BD⊥B′D′,BD=B′D′.利用“8字型”证明∠DHD′=∠BAD=90°即可.
(3)分四种情形①如图3-1中,当0<x≤![]() 时,重叠部分是四边形ACDH.②如图3-2中,当
时,重叠部分是四边形ACDH.②如图3-2中,当![]() <x≤4时,重叠部分是五边形ACMNH.③如图3-2中,当
<x≤4时,重叠部分是五边形ACMNH.③如图3-2中,当![]() <x≤
<x≤![]() 时,重叠部分是五边形ACMNH.如图3-4中,当
时,重叠部分是五边形ACMNH.如图3-4中,当![]() <x<4+
<x<4+![]() 时,重叠部分是△BB′H.分别求解即可.
时,重叠部分是△BB′H.分别求解即可.
解:(1)如图1中,
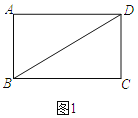
∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=![]() ,
,
∴tan∠ABD=![]() ,
,
∴∠ABD=60°,
故答案为:60.
(2)结论:BD⊥B′D′,BD=B′D′.
理由:如图2中,延长BD交D′B′于H.
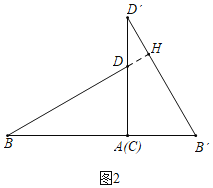
∵∠B=∠D′,∠BDA=∠HDD′,
∴∠BAD=∠DHD′=90°,
∴BD⊥B′D′.
∵BD与B′D′为矩形的对角线,则BD=B′D′;
故答案为:BD=B′D′,BD⊥B′D′.
(3)①如图3-1中,当0<x≤![]() 时,重叠部分是四边形ACDH,
时,重叠部分是四边形ACDH,
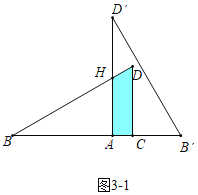
由题意:AB=![]() ,AH=
,AH=![]() AB=
AB=![]() ,
,
∵AH∥CD,
∴![]() ,
,
∴![]() ,
,
∴BH=![]() ,
,
∴DH=8-(![]() )=
)=![]() ,
,
y=x+4+![]()
=x+4+4![]()
=![]() ;
;
②如图3-2中,当![]() <x≤4时,重叠部分是五边形ACMNH.
<x≤4时,重叠部分是五边形ACMNH.
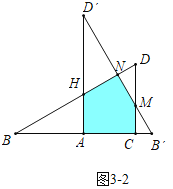
![]()
=![]()
=![]() ;
;
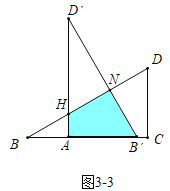
③如图3-3中,当4<x≤![]() 时,重叠部分是四边形AB′NH.
时,重叠部分是四边形AB′NH.
![]()
=![]()
=![]() ;
;
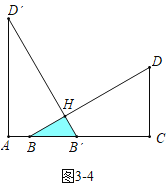
④如图3-4中,当![]() 时,重叠部分是△BB′H.
时,重叠部分是△BB′H.
![]()
![]()
![]() ;
;
故答案为: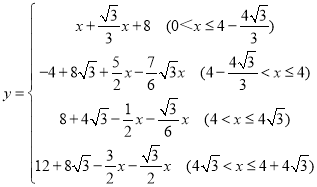 ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接边境贸易博览会,组织部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
-
科目: 来源: 题型:
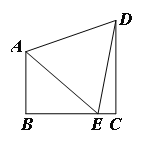
查看答案和解析>>【题目】如图,四边形ABCD,∠B=∠C=90°,边BC上一点E,连结AE、DE得等边△ABC,若
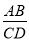 =
=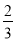 ,则
,则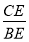 =_____
=_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
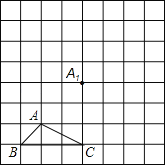
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,得到△A1B2C2,在网格中画出旋转后的△A1B2C2.
(3)连结
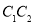 ,请判断
,请判断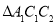 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC 中,AD 是 BC 边上的中线.
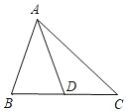
(1)画出与△ACD 关于点 D 成中心对称的三角形;
(2)找出与 AC 相等的线段;
(3)探索:△ABC 中,AB+AC 与中线 AD 之间的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在△ABC中,∠C=90°,∠BAC的平分线与外角∠CBE的平分线相交于点D,求∠D的度数.
(2)如图②,将(1)中的条件“
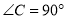 ”改为
”改为 ,其它条件不变,请直接写出
,其它条件不变,请直接写出 与
与 的数量关系.
的数量关系.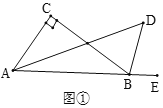

相关试题

