搜索
【题目】如图所示，正方形网格中，△ABC为格点三角形(即三角形的顶点都在格点上).
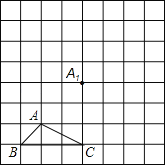
(1)把△ABC沿BA方向平移后，点A移到点A1，在网格中画出平移后得到的△A1B1C1；
(2)把△A1B1C1绕点A1按逆时针方向旋转90°，得到△A1B2C2，在网格中画出旋转后的△A1B2C2.
(3)连结
，请判断
的形状，并说明理由.
参考答案：
【答案】(1)见解析；(2)见解析；(3)
是等腰直角三角形
【解析】
(1)利用平移的性质得出对应点位置进而得出答案；
(2)利用旋转的性质进而得出旋转后对应点位置进而得出答案；
(3)根据旋转的性质进行判断即可.
(1)如图所示，
就是所求；
(2)如图所示，
就是所求；
(3) 是等腰直角三角形，理由如下：
由旋转性质可知：
，
是等腰直角三角形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为迎接边境贸易博览会，组织部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧，已知搭配一个A种造型需甲种花卉80盆，乙种花卉40盆，搭配一个B种造型需甲种花卉50盆，乙种花卉90盆．
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来．
(2)若搭配一个A种造型的成本是800元，搭配一个B种造型的成本是960元，试说明(1)中哪种方案成本最低？最低成本是多少元？
-
科目： 来源： 题型：
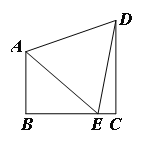
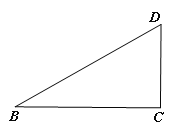
查看答案和解析>>【题目】如图，四边形ABCD，∠B＝∠C＝90°，边BC上一点E，连结AE、DE得等边△ABC，若
＝
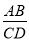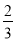，则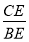
＝_____
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，矩形ABCD，AB＝4，BC＝
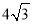．（1）直接写出：∠ABD＝______度；
（2）将矩形ABCD沿BD剪开得到两个三角形，按图2摆放：点A与点C重合，CD落在AD′上，直接写出BD与B′D′的关系：_____；
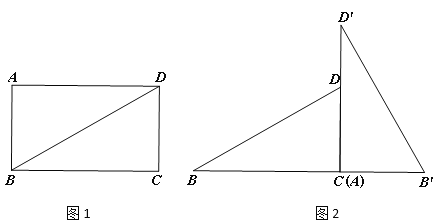
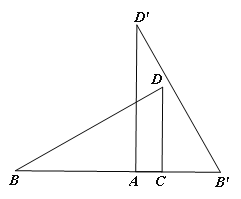
（3）在图2的基础上将△AB′D′向左平移，点B′与B重合停止，设AC＝x，两个三角形重合部分的封闭图形的周长为y，请用x表示y：____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在△ABC 中，AD 是 BC 边上的中线．
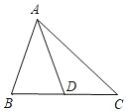
（1）画出与△ACD 关于点 D 成中心对称的三角形；
（2）找出与 AC 相等的线段；
（3）探索：△ABC 中，AB+AC 与中线 AD 之间的关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1)如图①，在△ABC中，∠C=90°，∠BAC的平分线与外角∠CBE的平分线相交于点D，求∠D的度数.
(2)如图②，将(1)中的条件“
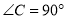”改为
，其它条件不变，请直接写出
与
的数量关系.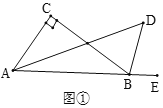
-
科目： 来源： 题型：
查看答案和解析>>【题目】威丽商场销售A、B两种商品，售出1件A种商品和4件B种商品所得利润为600元；售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元？
(2)由于需求量大，A、B两种商品很快售完，威丽商场决定再一次购进A、B两种商品共34件，如果将这34件商品全部售完后所得利润不低于4000元，那么威丽商场至少需购进多少件A种商品？
相关试题
