【题目】如图,已知矩形ABCD的对角线交于点E,将△DCB沿CD翻折得到△DCF.
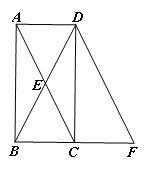
(1)求证:四边形ACFD是平行四边形;
(2)点H为DF的中点,连结CH,若AB=4,BC=2,求四边形ECHD的面积.
参考答案:
【答案】(1)见解析;(2)4
【解析】
(1)由矩形的性质得到AD∥BC,根据折叠的性质得到BC=CF,根据平行四边形的判定定理即可得到结论;
(2)根据三角形的面积公式得到S△BCD=S△FCD=![]() ×2×4=4,由矩形的性质得到E为BD中点,根据三角形的面积公式即可得到结论.
×2×4=4,由矩形的性质得到E为BD中点,根据三角形的面积公式即可得到结论.
(1)证明:
∵四边形ABCD为矩形,
∴AD∥BC
由翻折可知:BC=CF
∴AD∥CF
∴四边形ACFD为平行四边形
(2)解:∵AB=4,BC=CF=2
又∵DC⊥BF
∴S△BCD=S△FCD=![]() =4
=4
∴四边形ABCD为矩形
∴E为BD中点
∴S△CED=![]() S△BCD=2
S△BCD=2
∵H为DF的中点
∴S△CDH=![]() S△DCF=2
S△DCF=2
∴S四边形ECHD=S△CED+S△DHC=2+2=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC 中,AD 是 BC 边上的中线.
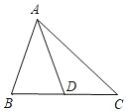
(1)画出与△ACD 关于点 D 成中心对称的三角形;
(2)找出与 AC 相等的线段;
(3)探索:△ABC 中,AB+AC 与中线 AD 之间的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在△ABC中,∠C=90°,∠BAC的平分线与外角∠CBE的平分线相交于点D,求∠D的度数.
(2)如图②,将(1)中的条件“
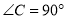 ”改为
”改为 ,其它条件不变,请直接写出
,其它条件不变,请直接写出 与
与 的数量关系.
的数量关系.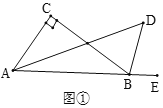

-
科目: 来源: 题型:
查看答案和解析>>【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在10×10网格中,点A和直线l的位置如图所示:

(1)将点A向右平移6个单位,再向上平移2个单位长度得到点B,在网格中标出点B;
(2)在(1)的条件下,在直线l上确定一点P,使PA+PB的值最小,保留画图痕迹,并直接写出PA+PB的最小值:______;
(3)结合(2)的画图过程并思考,直接写出
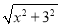 +
+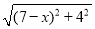 的最小值:____
的最小值:____ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,线段
,线段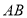 、
、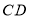 相交于
相交于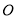 ,连结
,连结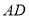 、
、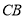 ,我们把形如图
,我们把形如图 的图形称之为“
的图形称之为“ ”字形,如图
”字形,如图 ,在图
,在图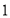 的条件下,
的条件下,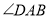 和
和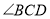 的平分线
的平分线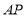 和
和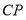 相交于点
相交于点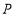 ,并且与
,并且与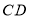 、
、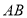 分别相交于
分别相交于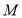 、
、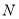 ,试解答下列问题:
,试解答下列问题: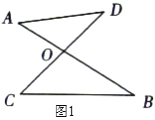
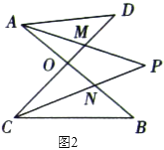
(1)在图
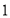 中,请直接写出
中,请直接写出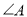 、
、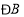 、
、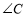 、
、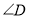 之间的数量关系:__________
之间的数量关系:__________(2)仔细观察,在图
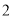 中“
中“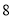 ”字形的个数:______个;
”字形的个数:______个;(3)图
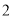 中,当
中,当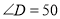 度,
度,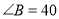 度时,求
度时,求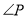 的度数.
的度数.(4)图
 中
中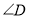 和
和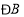 为任意角时,其它条件不变,试问
为任意角时,其它条件不变,试问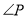 与
与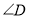 、
、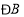 之间存在着怎样的数量关系?(直接写出结果,不必证明)
之间存在着怎样的数量关系?(直接写出结果,不必证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形ABCD,E为边AB上的点,将△BCE沿CE折叠,点B恰好落在AC上点B′处.

(1)若AB=8,BC=6,求BE的长度;
(2)如图2,过点D作EC的垂线,垂足为点G,分别交BC、AC于点F、H,连结EF,若EF=AE,求证:
 为定值;
为定值;(3)若四边形EFCH是菱形,则
 =_____.
=_____.
相关试题

