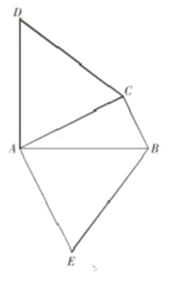
【题目】如图,在△ABC中,DA⊥AB,AD=AB,EA⊥AC,AE=AC.
(1)试说明△ACD≌△AEB;
(2)若∠ACB=90°,连接CE,
①说明EC平分∠ACB;
②判断DC与EB的位置关系,请说明理由.
参考答案:
【答案】(1)详见解析;(2)详见解析;
【解析】
(1)利用垂直证明∠DAC=∠EAB,即可证明全等;
(2)①根据AE=AC,∠ACB=90°,可得∠ACE=∠BCE=45°;
②延长DC交EB于F,先求出∠D=∠ABE,得到∠D+∠BAE+∠AEB=180°,再根据∠D+∠BAD+∠AEB+∠BAE+∠F=360°,求出∠F即可.
(1)∵DA⊥AB,EA⊥AC
∴∠DAB=∠CAE=90°
∴∠DAC+∠CAB=∠BAE+∠CAB
∴∠DAC=∠EAB
∵AD=AB,AE=AC
∴△ACD≌△AEB;
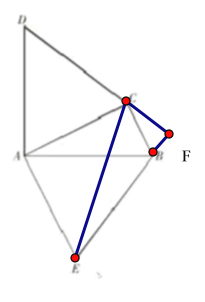
(2)①连接CE,∵DC⊥EB
∵EA⊥AC,AE=AC
∴∠ACE=∠CEA=45°
∵∠ACB=90°
∴∠BCE=45°=∠ACE
∴EC平分∠ACB
②延长DC交EB于F,
∵△ACD≌△AEB
∴∠D=∠ABE
∵∠ABE+∠BAE+∠AEB=180°
∴∠D+∠BAE+∠AEB=180°
∵∠D+∠BAD+∠AEB+∠BAE+∠F=360°
∴∠D+∠BAE+∠AEB+∠BAD+∠F=360°
∴180°+90°+∠F=360°
∴∠F=90°
∴DC⊥EB
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC(如图).
(1)利用尺规按下列要求作图(保留作图痕迹,不写作法):
①作∠BAC的平分线AD,交BC于点D;
②作AB边的垂直平分线EF,分别交AD,AB于点E,F.
(2)连接BE,若∠ABC=60°,∠C=40°,求∠AEB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.

(1)当x的取值为 时,在甲乙两家店所花钱一样多?
(2)当x的取值为 时,在乙店批发比较便宜?
(3)如果批发30千克该水果时,在甲店批发比在乙店批发便宜50元,求射线AB的表达式,并写出定义域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程m2x2+(2m﹣1)x+1=0有两个不相等的根a,b,
(1)求实数m的取值范围;
(2)是否存在实数m,使方程的两个实数根互为相反数?如果存在求出m的值,如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)点G抛物线上的动点,在x轴上是否存在点E,使B、D、E、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的E点坐标;如果不存在,请说明理由.

-
科目: 来源: 题型:
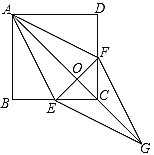
查看答案和解析>>【题目】如图,正方形
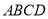 中,点
中,点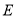 、
、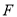 分别在边
分别在边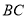 、
、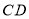 上,
上,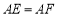 ,
,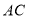 和
和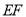 交于点
交于点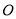 ,延长
,延长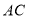 至点
至点 ,使得
,使得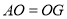 ,联结
,联结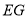 、
、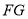 .
.
(1)求证:
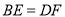 ;
;(2)求证:四边形
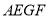 是菱形.
是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=60°.在△ABC的外侧作直线AP,点C关于直线AP的对称点为D,连接AD,BD.
(1)依据题意补全图形;
(2)当∠PAC等于多少度时,AD∥BC?请说明理由;
(3)若BD交直线AP于点E,连接CE,求∠CED的度数;
(4)探索:线段CE,AE和BE之间的数量关系,并说明理由.

相关试题

