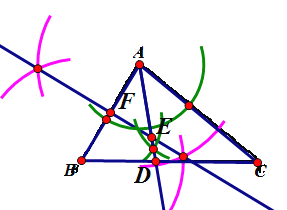
【题目】已知,△ABC(如图).
(1)利用尺规按下列要求作图(保留作图痕迹,不写作法):
①作∠BAC的平分线AD,交BC于点D;
②作AB边的垂直平分线EF,分别交AD,AB于点E,F.
(2)连接BE,若∠ABC=60°,∠C=40°,求∠AEB的度数.

参考答案:
【答案】(1)详见解析;(2)100°
【解析】
(1)①利用基本作图法作∠BAC的平分线AD;
②利用基本作图法作出AB边的垂直平分线EF;
(2)根据题意求出∠BAE=40°,因为EF为AB的垂直平分线,所以AE=BE,可得∠BAE=40°=∠ABE,即可求解.
(1)①AD为所求直线;
②EF为所求直线;
(2)
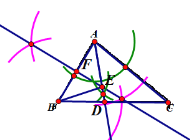
∵∠ABC=60°,∠C=40°
∴∠BAC==80°
∵AD平分∠BAC
∴∠BAE=40°
∵EF为AB的垂直平分线
∴AE=BE
∴∠BAE=40°=∠ABE
∴∠AEB=100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由正比例函数
 沿
沿 轴的正方向平移4个单位而成的一次函数
轴的正方向平移4个单位而成的一次函数
的图像与反比例函数
 (
( )在第一象限的图像交于A(1,n)和B两点.
)在第一象限的图像交于A(1,n)和B两点.(1)求一次函数
 和反比例函数的解析式;
和反比例函数的解析式;(2)求△ABO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)x2﹣3x+2=0
(2)(x+3)(x﹣6)=﹣8
(3)(2x+1)2=3(2x+1)
(4)2x2﹣x﹣15=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.

(1)当x的取值为 时,在甲乙两家店所花钱一样多?
(2)当x的取值为 时,在乙店批发比较便宜?
(3)如果批发30千克该水果时,在甲店批发比在乙店批发便宜50元,求射线AB的表达式,并写出定义域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程m2x2+(2m﹣1)x+1=0有两个不相等的根a,b,
(1)求实数m的取值范围;
(2)是否存在实数m,使方程的两个实数根互为相反数?如果存在求出m的值,如果不存在,请说明理由.
-
科目: 来源: 题型:
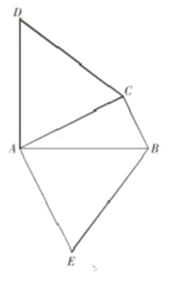
查看答案和解析>>【题目】如图,在△ABC中,DA⊥AB,AD=AB,EA⊥AC,AE=AC.
(1)试说明△ACD≌△AEB;
(2)若∠ACB=90°,连接CE,
①说明EC平分∠ACB;
②判断DC与EB的位置关系,请说明理由.
相关试题

