【题目】如图,在△ABC中,AB=AC,∠BAC=60°.在△ABC的外侧作直线AP,点C关于直线AP的对称点为D,连接AD,BD.
(1)依据题意补全图形;
(2)当∠PAC等于多少度时,AD∥BC?请说明理由;
(3)若BD交直线AP于点E,连接CE,求∠CED的度数;
(4)探索:线段CE,AE和BE之间的数量关系,并说明理由.

参考答案:
【答案】(1)详见解析;(2)30°;(3)120(4)![]()
【解析】
(1)根据题意画出图形即可;
(2)连接CD,交AP于CD于F,因为AD∥BC,所以∠C=∠CAD,由对称可得AC=AD,CF=FD,AF⊥CD,所以AP平分∠CAD,即可求解.
(3)AD=AC,∠DAP=∠CAP,∠DEP=∠PEC,求出AB=AC=AD,得到∠ABE=∠D,在△ABE中,得∠ABE+∠AEB+∠BAE=180°,得到∠D+∠CAE+60°+∠D+∠CAE =180°,求出∠D+∠CAE=60°,证明∠DEP=60°,即可求解;
(4)CE +AE=BE,如图,在BE上取点M使ME=AE,连接AM,设∠EAC=∠DAE=x,求得∠AEB=60°,从而得到△AME为等边三角形,根据等边三角形的性质和SAS即可判定△AEC≌△AMB,根据全等三角形的性质可得CE=BM,由此即可证得CE+AE=BE.
(1)
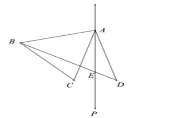
(2)连接CD,交AP于F,

∵AB=AC,∠BAC=60°
∴等边三角形ABC
∴∠BCA=60°
∵AD∥BC
∴∠BCA=60°=∠DAC
由对称可得AC=AD,CF=FD,AF⊥CD
∴AP平分∠CAD
∴∠PAC=30°
(3)由对称可得AD=AC,∠DAE=∠CAE,∠DEP=∠PEC
∵等边三角形ABC
∴AB=AC=AD
∴∠ABE=∠D
∵△ABE
∴∠ABE+∠AEB+∠BAE=180°
∴∠ABE+∠AEB+∠BAC+∠CAE=180°
∴∠D+∠CAE+60°+∠D+∠CAE =180°
∴∠D+∠CAE=60°
∴∠DEP=60°
∴∠DEC=120°;

(4)CE+AE=BE.
在BE上取点M使ME=AE,连接AM,
在等边△ABC中,
AC=AB,∠BAC=60°
由对称可知:AC=AD,∠EAC=∠EAD,
设∠EAC=∠DAE=x.
∵AD=AC=AB,
∴∠D=60°-x
∴∠AEB=60-x+x=60°.
∴△AME为等边三角形.
∴AM=AE,∠MAE=60°,
∴∠BAC=∠MAE=60°,
即可得∠BAM=∠CAE.
在△AMB和△AEC中,AB=AC,∠BAM=∠CAE, AM=AE,
∴△AMB≌△AEC.
∴CE=BM.
∴CE+AE=BE.
-
科目: 来源: 题型:
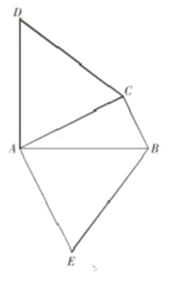
查看答案和解析>>【题目】如图,在△ABC中,DA⊥AB,AD=AB,EA⊥AC,AE=AC.
(1)试说明△ACD≌△AEB;
(2)若∠ACB=90°,连接CE,
①说明EC平分∠ACB;
②判断DC与EB的位置关系,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)点G抛物线上的动点,在x轴上是否存在点E,使B、D、E、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的E点坐标;如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,点
中,点 、
、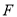 分别在边
分别在边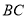 、
、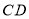 上,
上,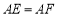 ,
,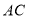 和
和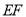 交于点
交于点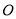 ,延长
,延长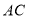 至点
至点 ,使得
,使得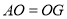 ,联结
,联结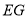 、
、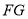 .
.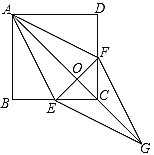
(1)求证:
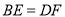 ;
;(2)求证:四边形
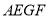 是菱形.
是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:
①abc>0;②b2=4ac; ③4a+2b+c>0;④3a+c>0,

其中,正确的结论是______.(写出正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交车每天的支出费用为60 元,每天的乘车人数 x(人)与每天利润(利润 =票款收入 -支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人)
…
200
250
300
350
400
…
y(元)
…
-20
-10
0
10
20
…
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为 5 00人时,利润是多少?
(4) 试写出该公交车每天利润 y(元)与每天乘车人数x (人)的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A. 对我市市民实施低碳生活情况的调查
B. 对我国首架大型民用飞机零部件的检查
C. 对全国中学生心理健康现状的调查
D. 对市场上的冰淇淋质量的调查
相关试题

