搜索
【题目】已知抛物线y=ax2+bx﹣8（a≠0）的对称轴是直线x=1，
（1）求证：2a+b=0；
（2）若关于x的方程ax2+bx﹣8=0，有一个根为4，求方程的另一个根．
参考答案：
【答案】
（1）解：∵抛物线的对称轴是x=1，
∴ 
=1，
∴2a+b=0
（2）解：∵关于x的方程ax2+bx﹣8=0有一个根为4，
∴抛物线y=ax2+bx﹣8（a≠0）与x轴的一个交点坐标为（4，0），
∵抛物线的对称轴是x=1，
∴抛物线y=ax2+bx﹣8（a≠0）与x轴的另一个交点坐标为（﹣2，0），
∴关于x的方程ax2+bx﹣8=0，有一个根为﹣2．
【解析】（1）根据对称轴是直线x=1=-
，即可得出结论。
（2）先根据二次函数的性质、对称轴及与x轴的一个交点坐标，求出抛物线与x轴的另一个交点坐标，再根据抛物线y=ax2+bx﹣8与x轴的两交点的横坐标就是关于x的方程ax2+bx﹣8=0两个根。即可求解。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知
ABCD 中，∠BDC＝45°，BE⊥CD 于 E，DG⊥BC 于 G，BE、DG 相交于 H，DG、AB 的延长线 相交于 F，下面结论：①∠A＝∠DHE；②△DCG≌△BCE；③AD＝DH；④DH=HF其中正确的结论有________（只填正确结论的序号）． 
-
科目： 来源： 题型：
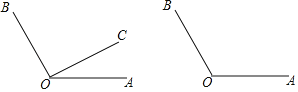
查看答案和解析>>【题目】如图，∠AOB＝120°，点C为平面内一点，作射线OC，射线OD平分∠BOC，射线OE平分∠AOD．
（1）若点C为∠AOB内部一点且∠AOC＝30°，依题意补全图形，并求出∠EOC的度数；
（2）若点C为∠AOB内部一点，∠AOC＝α（0＜α＜120°）直接用含α的代数式表示∠EOC的度数；
（3）若∠EOC＝10°，请你直接写出所有符合条件的∠AOC度数（0＜∠AOC＜180°）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平行四边形 ABCD 的对角线 AC、BD 交于 O 点，AE∥BD，∠AED＝∠AOD，连接 OE．
（1）求证：AE＝OB；
（2）求证：四边形 CDEO 是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系上有点A（1，0），点A第一次跳动至点A1（-1，1），第二次跳动至点A2（2，1），第三次跳动至点A3（-2，2），第四次向右跳动5个单位至点A4（3，2），………，依此规律跳动下去，点A第100次跳动至点A100的坐标是________；
-
科目： 来源： 题型：
查看答案和解析>>【题目】现有一个种植总面积为540m2的矩形塑料温棚，分垄间隔套种草莓和西红柿共24垄，种植的草莓或西红柿单种农作物的总垄数不低于10垄，又不超过14垄(垄数为正整数)，它们的占地面积、产量、利润分别如下：
占地面积（m/垄）
产量（千克/垄）
利润（元/千克）
西红柿
30
160
1.1
草莓
15
50
1.6
（1）若设草莓共种植了
垄，通过计算说明共有几种种植方案？分别是哪几种？（2）在这几种种植方案中，哪种方案获得的利润最大？最大利润是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，若△ABC和△ADE为等边三角形，M，N分别是BE，CD的中点，
（1）求证：△AMN是等边三角形．
（2）当把△ADE绕A点旋转到图2的位置时，CD=BE是否仍然成立？若成立请证明，若不成立请说明理由．
相关试题
