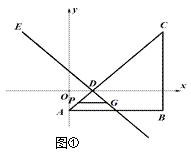
【题目】如图①,等腰直角三角形ABC的顶点A的坐标为 ![]() ,C的坐标为
,C的坐标为 ![]() ,直角顶点B在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.
,直角顶点B在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.
(1)直接写出点B、D、E的坐标并求出直线DE的解析式.
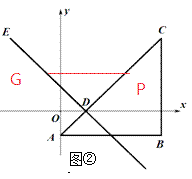
(2)如图②,点P以每秒1个单位的速度沿线段AC从点A运动到点C的过程中,过点P作与x轴平行的直线PG,交直线DE于点G,求与△DPG的面积S与运动时间t的函数关系式,并求出自变量t的取值范围.
(3)如图③,设点F为直线DE上的点,连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FE以每秒 ![]() 个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.
个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:由题意得:B(4,-1),D(1,0).E(-2,3)
设直线DE为 ![]()
![]()
把D(1,0).E(-2,3)代入得
![]()
解之得: ![]()
∴直线DE为: ![]()
(2)解:在Rt△ABC中,由 ![]()
![]() ,
,
由 ![]()
![]()
同理可得: ![]()
由题意可知: ![]() ,∠DPG=∠DAB=45°
,∠DPG=∠DAB=45°
∴△DPG为等腰直角三角形
![]()
①当 ![]() 时
时
∴ ![]()
![]()
②当 ![]() 时,
时,
易得 ![]()
![]()
综上: ![]() (
( ![]() )
)
(3)解:如图③,易得∠EDO=45°.
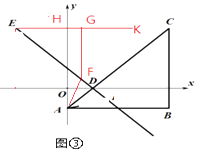
过点E作EK∥x轴交 ![]() 轴于H,则∠KEF=∠EDO=45°.
轴于H,则∠KEF=∠EDO=45°.
过点F作FG⊥EK于点G,则FG=EG= ![]() .
.
由题意,动点M运动的路径为折线AF+EF,运动时间:
![]() ,
,
∴ ![]() ,即运动时间等于折线AF+FG的长度.
,即运动时间等于折线AF+FG的长度.
由垂线段最短可知,折线AF+FG的长度的最小值为EK与线段AB之间的垂线段.
则t最小=AH,AH与 ![]() 轴的交点,即为所求之F点.
轴的交点,即为所求之F点.
∵直线DE解析式为: ![]()
∴F(0,1).
综上所述,当点F坐标为(0,1)时,点M在整个运动过程中用时最少
【解析】(1)根据坐标的定义结合题意可得B、D、E的坐标,利用待定系数法即可求出直线DE的解析式即可。
(2)先根据勾股定理分别求出AC、AD的长,再证明△DPG为等腰直角三角形,得出 s=![]() DP2 .分两种情况:①当 0 ≤ t ≤
DP2 .分两种情况:①当 0 ≤ t ≤![]() 时;②当
时;②当![]() < t ≤ 4
< t ≤ 4![]() 时,分别求出DP的长,即可得出结果。
时,分别求出DP的长,即可得出结果。
(3)过点E作EK∥x轴交y轴于H,则∠KEF=∠EDO=45°.过点F作FG⊥EK于点G,则FG=EG=![]() EF,由题意,动点M运动的路径为折线AF+EF,运动时间:t=AF+EF,推出t=AF+FG,即运动时间等于折线AF+FG的长度,由垂线段最短可知,折线AF+FG的长度的最小值为EK与线段AB之间的垂线段.则t最小=AH,直线DE与y轴的交点即为所求之F点。
EF,由题意,动点M运动的路径为折线AF+EF,运动时间:t=AF+EF,推出t=AF+FG,即运动时间等于折线AF+FG的长度,由垂线段最短可知,折线AF+FG的长度的最小值为EK与线段AB之间的垂线段.则t最小=AH,直线DE与y轴的交点即为所求之F点。
-
科目: 来源: 题型:
查看答案和解析>>【题目】点 P(﹣7,3)是由点M先向左平移动3个单位,再向下平移动3个单位而得到,则M的坐标为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,点P(-3,2)关于x轴对称点的坐标是( )
A. (3,2) B. (3,-2) C. (-3,2) D. (-3,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 中,
中, 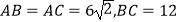 .点
.点 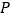 从点
从点 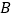 出发沿线段
出发沿线段 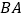 移动,同时点
移动,同时点 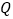 从点
从点 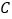 出发沿线段
出发沿线段 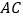 的延长线移动,点
的延长线移动,点 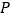 、
、 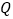 移动的速度相同,
移动的速度相同, 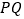 与直线
与直线 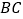 相交于点
相交于点 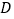 .
.
(1)如图①,当点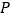 为
为 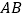 的中点时,求
的中点时,求 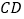 的长;
的长;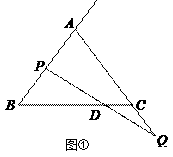
(2)如图②,过点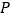 作直线
作直线 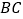 的垂线,垂足为
的垂线,垂足为 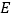 ,当点
,当点 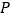 、
、 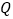 在移动的过程中,设
在移动的过程中,设 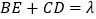 ,
, 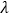 是否为常数?若是请求出
是否为常数?若是请求出 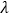 的值,若不是请说明理由.
的值,若不是请说明理由.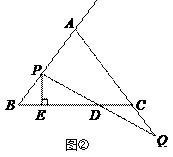
(3)如图③,E为BC的中点,直线CH垂直于直线AD,垂足为点H,交AE的延长线于点M;直线BF垂直于直线AD,垂足为F;找出图中与BD相等的线段,并证明.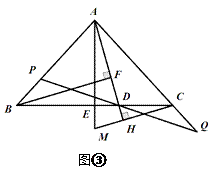
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式(x+y)2﹣3(x+y)的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的内角和比外角和多180°,那么这个多边形是( )
A.四边形B.五边形C.六边形D.七边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的解析式为
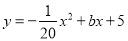 .
.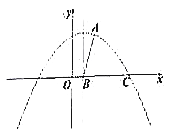
(1)当自变量
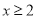 时,函数值
时,函数值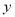 随
随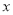 的增大而减少,求
的增大而减少,求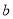 的取值范围;
的取值范围;(2)如图,若抛物线的图象经过点
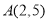 ,与
,与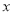 轴交于点
轴交于点 ,抛物线的对称轴与
,抛物线的对称轴与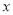 轴交于
轴交于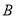 .
.①求抛物线的解析式;
②在抛物线上是否存在点
 ,使得
,使得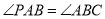 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

