【题目】已知 ![]() 中,
中, ![]() .点
.点 ![]() 从点
从点 ![]() 出发沿线段
出发沿线段 ![]() 移动,同时点
移动,同时点 ![]() 从点
从点 ![]() 出发沿线段
出发沿线段 ![]() 的延长线移动,点
的延长线移动,点 ![]() 、
、 ![]() 移动的速度相同,
移动的速度相同, ![]() 与直线
与直线 ![]() 相交于点
相交于点 ![]() .
.
(1)如图①,当点 ![]() 为
为 ![]() 的中点时,求
的中点时,求 ![]() 的长;
的长;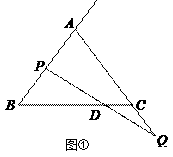
(2)如图②,过点 ![]() 作直线
作直线 ![]() 的垂线,垂足为
的垂线,垂足为 ![]() ,当点
,当点 ![]() 、
、 ![]() 在移动的过程中,设
在移动的过程中,设 ![]() ,
, ![]() 是否为常数?若是请求出
是否为常数?若是请求出 ![]() 的值,若不是请说明理由.
的值,若不是请说明理由.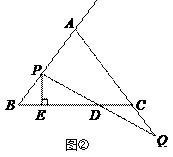
(3)如图③,E为BC的中点,直线CH垂直于直线AD,垂足为点H,交AE的延长线于点M;直线BF垂直于直线AD,垂足为F;找出图中与BD相等的线段,并证明.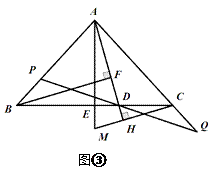
参考答案:
【答案】
(1)解:如图,过P点作PF∥AC交BC于F,
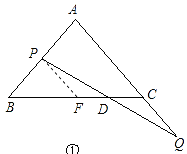
∵点P和点Q同时出发,且速度相同,
∴BP=CQ,
∵PF∥AQ,
∴∠PFB=∠ACB,∠DPF=∠CQD,
又∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠PFB,
∴BP=PF,
∴PF=CQ,又∠PDF=∠QDC,
∴△PFD≌△QCD,
∴DF=CD= ![]() CF,
CF,
又因P是AB的中点,PF∥AQ,
∴F是BC的中点,即FC= ![]() BC=6,
BC=6,
∴CD= ![]() CF=3
CF=3
(2)解: ![]() 为定值.
为定值.
如图②,点P在线段AB上,过点P作PF∥AC交BC于F,
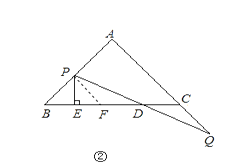
易知△PBF为等腰三角形,
∵PE⊥BF
∴BE= ![]() BF
BF
∵易得△PFD≌△QCD
∴CD= ![]()
∴ ![]()
(3)解:BD=AM
证明:∵ ![]()
∴ ![]()
∴ ![]()
∵E为BC的中点
∴ ![]()
∴ ![]() ,
, ![]()
∴ ![]() ,
, ![]()
∵AH⊥CM
∴ ![]()
∵ ![]()
∴ ![]()
∴ ![]() ≌
≌ ![]() (ASA)
(ASA)
∴ ![]()
∴ ![]()
即: ![]()
【解析】(1)根据已知可知BP=CQ,再根据PF∥AQ及AB=AC,证明∠B=∠PFB,得出BP=PF,证得PF=CQ,然后根据角角边证明△PFD≌△QCD,得出DF=CD=![]() CF,根据已知P是AB的中点,PF∥AQ,证明点F是BC的中点,求出CF的长,即可求出CD的长。
CF,根据已知P是AB的中点,PF∥AQ,证明点F是BC的中点,求出CF的长,即可求出CD的长。
(2)点P在线段AB上,过点P作PF∥AC交BC于F,先证明△PBF为等腰三角形,根据PE⊥BF,得出BE与线段BF的数量关系,再证明△PFD≌△QCD ,结合CD= ![]() C F,然后根据B E + C D =
C F,然后根据B E + C D =![]() BC,即可得出结论。
BC,即可得出结论。
(3)先根据勾股定理的逆定理证明ΔABC是等腰直角三角形, 再根据E为BC的中点,去证明AE=EC,∠EAD = ∠ECM,然后证明△AED≌△CEM,得出DE=ME,根据BD=DE+BE=AE+ME=AM。即可得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在某标准游泳池相邻泳道进行100米自由泳训练,如图是他们各自离出发点的距离y(米)与他们出发的时间x(秒)的函数图象.根据图象,解决如下问题.(注标准泳池单向泳道长50米,100米自由泳要求运动员在比赛中往返一次;返回时触壁转身的时间,本题忽略不计).
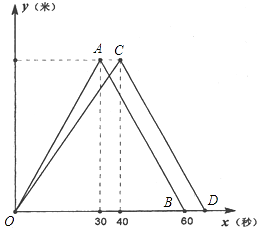
(1)直接写出点A坐标,并求出线段OC的解析式;
(2)他们何时相遇?相遇时距离出发点多远?
(3)若甲、乙两人在各自游完50米后,返回时的速度相等;则快者到达终点时领先慢者多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】点 P(﹣7,3)是由点M先向左平移动3个单位,再向下平移动3个单位而得到,则M的坐标为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,点P(-3,2)关于x轴对称点的坐标是( )
A. (3,2) B. (3,-2) C. (-3,2) D. (-3,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,等腰直角三角形ABC的顶点A的坐标为
 ,C的坐标为
,C的坐标为  ,直角顶点B在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.
,直角顶点B在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.
(1)直接写出点B、D、E的坐标并求出直线DE的解析式.
(2)如图②,点P以每秒1个单位的速度沿线段AC从点A运动到点C的过程中,过点P作与x轴平行的直线PG,交直线DE于点G,求与△DPG的面积S与运动时间t的函数关系式,并求出自变量t的取值范围.
(3)如图③,设点F为直线DE上的点,连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FE以每秒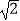 个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.
个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式(x+y)2﹣3(x+y)的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的内角和比外角和多180°,那么这个多边形是( )
A.四边形B.五边形C.六边形D.七边形
相关试题

